题目内容
等比数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列.
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:bn=an+(-1)nln an,求数列{bn}的前2n项和S2n.
解:(1)当a1=3时,不合题意;
当a1=2时,当且仅当a2=6,a3=18时,符合题意;
当a1=10时,不合题意.
因此a1=2,a2=6,a3=18,所以公比q=3.
故an=2·3n-1.
(2)因为bn=an+(-1)nln an,
=2×3n-1+(-1)nln(2×3n-1)
=2×3n-1+(-1)n[ln 2+(n-1)ln 3]
=2×3n-1+(-1)n(ln 2-ln 3)+(-1)nn ln 3.
所以S2n=b1+b2+…+b2n=2(1+3+…+32n-1)+[-1+1-1+…+(-1)2n](ln 2-ln 3)+[-1+2-3+…+(-1)2n2n]ln 3=2× +nln 3=32n+nln 3-1.
+nln 3=32n+nln 3-1.

练习册系列答案
相关题目
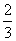 或
或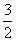 B.
B.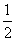 或2 D.
或2 D.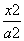 -
-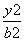 =1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为
=1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为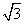 ,则p=( )
,则p=( )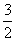 C.2 D.3
C.2 D.3 ,则{an}的前10项和等于( )
,则{an}的前10项和等于( ) (1-310)
(1-310)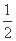 ,a4=4,则公比q= ;a1+a2+…+an= .
,a4=4,则公比q= ;a1+a2+…+an= .  为等比数列,并求数列{bn}的通项公式.
为等比数列,并求数列{bn}的通项公式.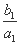 +
+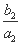 +…+
+…+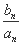 =1-
=1-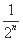 ,n∈N* ,求{bn}的前n项和Tn.
,n∈N* ,求{bn}的前n项和Tn. 则该函数是( )
则该函数是( )