题目内容
(本题满分12分)己知斜三棱柱 的底面是边长为
的底面是边长为 的正三角形,侧面
的正三角形,侧面 为菱形,
为菱形, ,平面
,平面 平面
平面 ,
, 是
是 的中点.
的中点.

(1)求证:
 ;
;
(2)求二面角 的余弦值.
的余弦值.
(1)证明见解析;(2) .
.
【解析】
试题分析:(1)解决立体几何的有关问题,空间想象能力是非常重要的,但新旧知识的迁移融合也很重要,在平面几何的基础上,把某些空间问题转化为平面问题来解决,有时很方便;(2)利用已知的线面垂直关系建立空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键,证明证线线垂直,只需要证明直线的方向向量垂直;(3)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(4)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:(1)取 的中点
的中点 ,连结
,连结 ,
, , 由题意知
, 由题意知  ,
, .
.
又因为 平面 平面
平面 ,所以
,所以  平面
平面
以 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系  . 2分
. 2分

则 ,
, ,
, ,
, ,
, ,
,
 .
.  4分
4分
因为  ,所以
,所以 6分
6分
(2)取 的中点
的中点 ,连结
,连结 ,
, , 由题意知
, 由题意知  ,
, .
.
又因为 平面 平面
平面 ,所以
,所以  平面
平面
以 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系  . 7分
. 7分
则 ,
, ,
, ,
, ,
, ,
,
 .
.
设平面 的法向量为
的法向量为 ,则
,则 即
即
令 .所以
.所以 . 9分
. 9分
又平面 的法向量
的法向量 10分
10分
设二面角 的平面角为
的平面角为 ,则
,则 . 12分
. 12分
考点:1、直线与直线垂直的判定;2、平面与平面所成角的余弦值.
考点分析: 考点1:点、线、面之间的位置关系 考点2:异面直线所成的角 考点3:线面所成的角 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
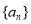 中,已知
中,已知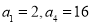 .
.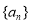 的通项公式.
的通项公式.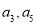 分别为等差数列
分别为等差数列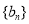 的第3项和第5项,试求数列
的第3项和第5项,试求数列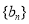 的前
的前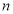 项和
项和 .
.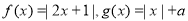
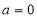 时,解不等式
时,解不等式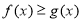 ;
; ,使得,
,使得,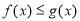 成立,求实数
成立,求实数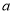 的取值范围.
的取值范围. 中,
中, ,则数列
,则数列 的前8项和等于( )
的前8项和等于( )
 时,解不等式
时,解不等式 ;
; ,使得,
,使得, 成立,求实数
成立,求实数 的取值范围.
的取值范围.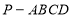 的五个顶点在同一球面上,若正四棱锥的底面边长是
的五个顶点在同一球面上,若正四棱锥的底面边长是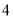 ,侧棱长为
,侧棱长为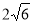 ,则此球的表面积___________.
,则此球的表面积___________. 满足不等式组
满足不等式组 则
则 的最大值是( )
的最大值是( ) B.
B. C.
C. D.
D.
 的两个极值点分别为
的两个极值点分别为 ,且
,且 ,点
,点 表示的平面区域内存在点
表示的平面区域内存在点 满足
满足 ,则实数
,则实数 的取值范围是
的取值范围是 B.
B.
 D.
D.
 ,已知
,已知 ,若关于
,若关于 的方程
的方程 恰有三个互不相等的实根
恰有三个互不相等的实根 ,则
,则 的取值范围是 。
的取值范围是 。