题目内容
(本小题满分l0分)选修4—5:不等式选讲
已知函数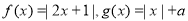
(1)当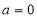 时,解不等式
时,解不等式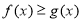 ;
;
(2)若存在 ,使得,
,使得,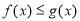 成立,求实数
成立,求实数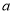 的取值范围.
的取值范围.
(1) ;(2)
;(2)
【解析】
试题分析:(1)理解绝对值的几何意义, 表示的是数轴的上点
表示的是数轴的上点 到原点离.(2)对于恒成立的问题,常用到以下两个结论:(1)
到原点离.(2)对于恒成立的问题,常用到以下两个结论:(1) 恒成立
恒成立 ,(2)
,(2) 恒成立
恒成立
(3) 的应用.(4)掌握一般不等式的解法:
的应用.(4)掌握一般不等式的解法: ,
, .
.
试题解析:当 时,由
时,由 得
得 ,两边平方整理得
,两边平方整理得 ,
,
解得 或
或 ,因此原不等式的解集为
,因此原不等式的解集为
由 得
得 ,令
,令 ,则
,则

故 ,从而所求实数
,从而所求实数 的范围
的范围 .
.
考点:1、含绝对值不等式的解法;2、恒成立的问题.
考点分析: 考点1:含绝对值的不等式 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ,
, ,则集合
,则集合 ( )
( ) B.
B. C.
C. D.
D.
 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 =
=
 .则
.则
 B.
B. C.
C. D.
D.
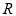 上的可导函数
上的可导函数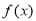 的导函数为
的导函数为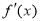 ,满足
,满足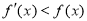 ,且
,且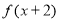 为偶函数,
为偶函数,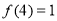 ,则不等式
,则不等式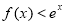 的解集为
的解集为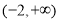 B.
B.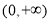
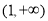 D.
D.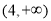
 的前
的前 项和为
项和为 ,若
,若 ,则
,则
 B.
B. C.
C. D.
D.
 、边长为
、边长为 的菱形,又
的菱形,又 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
 平面PAD;
平面PAD;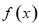 是定义在
是定义在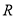 上的恒不为零的函数,对任意实数
上的恒不为零的函数,对任意实数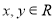 ,都有
,都有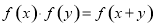 ,若
,若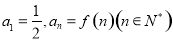 ,则数列
,则数列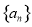 的前
的前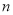 项和
项和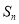 的取值范围是( )
的取值范围是( )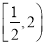 B.
B. 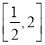 C.
C. 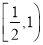 D.
D. 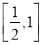
 的底面是边长为
的底面是边长为 的正三角形,侧面
的正三角形,侧面 为菱形,
为菱形, ,平面
,平面 平面
平面 ,
, 是
是 的中点.
的中点.

 ;
; 的余弦值.
的余弦值. 的不等式:
的不等式: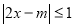 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.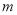 的值;
的值;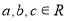 ,若
,若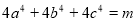 ,求
,求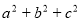 的最大值.
的最大值.