题目内容
5.已知数列{an}的各项都为正数,且对任意n∈N*,都有$a_{n+1}^2={a_n}{a_{n+2}}+k$(k为常数).(1)若k=0,且a1=1,-8a2,a4,a6成等差数列,求数列{an}的前n项和Sn;
(2)若$k={({a_2}-{a_1})^2}$,求证:a1,a2,a3成等差数列;
(3)已知a1=a,a2=b(a,b为常数),是否存在常数λ,使得an+an+2=λan+1对任意n∈N*都成立?若存在.求出λ;若不存在,说明理由.
分析 (1)利用等差数列与等比数列的通项公式及其求和公式即可得出.
(2)当$k={({a_2}-{a_1})^2}$时,$a_{n+1}^2={a_n}{a_{n+2}}+{({a_2}-{a_1})^2},n∈{N^*}$,令n=1,即可证明.
(3)存在常数$λ=\frac{{{a^2}+{b^2}-k}}{ab}$使得an+an+2=λan+1对任意n∈N*都成立.证明如下:令${b_n}=\frac{{{a_n}+{a_{n+2}}}}{{{a_{n+1}}}}$,对任意n∈N*,都有$a_{n+1}^2={a_n}{a_{n+2}}+k$,可得$\frac{{a_{n+1}^2+{a_{n+1}}{a_{n+3}}}}{{{a_{n+1}}{a_{n+2}}}}=\frac{{a_{n+2}^2+{a_n}{a_{n+2}}}}{{{a_{n+1}}{a_{n+2}}}}$,可得:bn+1=bn,n∈N*,进而得出.
解答 解:(1)当k=0时,$a_{n+1}^2={a_n}{a_{n+2}},n∈{N^*}$,
∵an>0,∴数列{an}为等比数列,设公比为q(q>0),
∵-8a2,a4,a6成等差数列,∴-8a2+a6=2a4,∴$-8{a_2}+{a_2}{q^4}=2{a_2}{q^2}$,
∵a2≠0,∴q4-2q2-8=0,∴q2=4,∴q=2.
∵a1=1,数列{an}的前n项和${S_n}=\frac{{1-{2^n}}}{1-2}={2^n}-1$.
(2)当$k={({a_2}-{a_1})^2}$时,$a_{n+1}^2={a_n}{a_{n+2}}+{({a_2}-{a_1})^2},n∈{N^*}$,
令n=1,则$a_2^2={a_1}{a_3}+{({a_2}-{a_1})^2}$,∴${a_1}{a_3}-2{a_1}{a_2}+{a_1}^2=0$,
∵a1>0,∴a1+a3-2a2=0,∴a1,a2,a3成等差数列.
(3)存在常数$λ=\frac{{{a^2}+{b^2}-k}}{ab}$使得an+an+2=λan+1对任意n∈N*都成立.
证明如下:令${b_n}=\frac{{{a_n}+{a_{n+2}}}}{{{a_{n+1}}}}$,∵对任意n∈N*,都有$a_{n+1}^2={a_n}{a_{n+2}}+k$,①,
k为常数,∴$a_{n+2}^2={a_{n+1}}{a_{n+3}}+k$,②
②-①得:$a_{n+2}^2-a_{n+1}^2={a_{n+1}}{a_{n+3}}-{a_n}{a_{n+2}}$,∴$a_{n+1}^2+{a_{n+1}}{a_{n+3}}=a_{n+2}^2+{a_n}{a_{n+2}}$.
∵an>0,∴an+1an+2>0∴$\frac{{a_{n+1}^2+{a_{n+1}}{a_{n+3}}}}{{{a_{n+1}}{a_{n+2}}}}=\frac{{a_{n+2}^2+{a_n}{a_{n+2}}}}{{{a_{n+1}}{a_{n+2}}}}$,
即:$\frac{{{a_{n+1}}+{a_{n+3}}}}{{{a_{n+2}}}}=\frac{{{a_n}+{a_{n+2}}}}{{{a_{n+1}}}}$,亦即:bn+1=bn,n∈N*,
∴数列{bn}为常数列,∴bn=b1,n∈N*,
∵a1=a,a2=b,$a_{n+1}^2={a_n}{a_{n+2}}+k$,n∈N*,
令n=1,则b2=aa3+k,∴${a_3}=\frac{{{b^2}-k}}{a}$,∴${b_n}={b_1}=\frac{{{a_1}+{a_3}}}{a_2}=\frac{{{a^2}+{b^2}-k}}{ab}$,n∈N*,
∴${a_n}+{a_{n+2}}=λ{a_{n+1}}?λ={b_n}=\frac{{{a^2}+{b^2}-k}}{ab}$,即存在常数$λ=\frac{{{a^2}+{b^2}-k}}{ab}$使得an+an+2=λan+1对任意n∈N*都成立.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于难题.

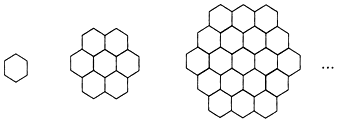 单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )
单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )| A. | 37 3n2-3n+1 | B. | 38 3n2-3n+2 | C. | 36 3n2-3n | D. | 35 3n2-3n-1 |
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
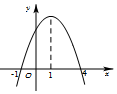
| A. | 在x=-1处取得极大值 | B. | 在区间[-1,4]上是增函数 | ||
| C. | 在x=1处取得极大值 | D. | 在区间[1,+∞)上是减函数 |