题目内容
9.从装有两个红球和三个黑球的口袋里任取两个球,那么互斥而不对立的两个事件是( )| A. | “至少有一个黑球”与“都是黑球” | |
| B. | “至少有一个黑球”与“至少有一个红球” | |
| C. | “恰好有一个黑球”与“恰好有两个黑球” | |
| D. | “至少有一个黑球”与“都是红球” |
分析 利用对立事件、互斥事件的定义求解.
解答 解:从装有两个红球和三个黑球的口袋里任取两个球,
在A中,“至少有一个黑球”与“都是黑球”能同时发生,不是互斥事件,故A错误;
在B中,“至少有一个黑球”与“至少有一个红球”能同时发生,不是互斥事件,故B错误;
在C中,“恰好有一个黑球”与“恰好有两个黑球”不能同时发生,
但能同时不发生,是互斥而不对立的两个事件,故C正确;
在D中,“至少有一个黑球”与“都是红球”是对立事件,故D错误.
故选:C.
点评 本题考查互斥而不对立事件的判断,是基础题,解题时要认真审题,注意对立事件、互斥事件的定义的合理运用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
19.下列有关命题的说法错误的为( )
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “|x|<2”是“x2-x-6<0”的充分不必要条件 | |
| C. | 命题“存在∈R,使得x2+x+1<0”的否定是“对任意x∈R,均有x2+x+1≥0” | |
| D. | 若p∧q为假命题,则p,q均为假 |
20.设a=log43,b=log34,c=log53,则( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | a>c>b |
17.过点M(1,1)的直线与椭圆$\frac{x^2}{12}+\frac{y^2}{9}=1$交于A,B两点,且点M平分弦AB,则直线AB方程为( )
| A. | 4x+3y-7=0 | B. | 3x+4y-7=0 | C. | 3x-4y+1=0 | D. | 4x-3y-1=0 |
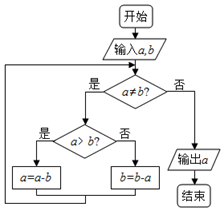 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为63,98,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为63,98,则输出的a=( )