题目内容
14.过点M(-2b,0)做椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两条切线,分别与椭圆交于A、B两点,且MA⊥MB,(1)求椭圆离心率;
(2)若椭圆的右焦点为F,四边形MAFB的面积为2+$\sqrt{2}$,求椭圆的标准方程.
分析 (1)利用垂直关系,求出直线的斜率,写出直线方程与椭圆联立,利用相切关系推出椭圆的离心率.
(2)表示出四边形的面积,然后转化求解b,即可得到椭圆的方程.
解答 解:(1)因为MA⊥MB所以kAM•kAN=-1,
由椭圆的对称性可知kAM=1,kAN=-1,…(2分)
设直线MA的方程 y=x+2b,联立$\left\{\begin{array}{l}y=x+2b\\ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\end{array}\right.$,消去y可得:(a2+b2)x2+4ba2x+3a2b2=0…(4分)
△=16b2a4-12a2b2(a2+b2)=0,
a2=3b2
$e=\sqrt{1-\frac{b^2}{a^2}}=\frac{{\sqrt{6}}}{3}$…(6分)
(2)${S_{四边形MAFB}}=2×\frac{1}{2}×|{MF}|×|{y_A}|$…(7分)
由(1)可知a2=3b2
则$2+\sqrt{2}=(2b+\sqrt{2}b){y_A}$,有${y_A}=\frac{1}{b}={x_A}+2b$
则${x_A}=\frac{1}{b}-2b$…(9分)
由(1)可知a2=3b2,则x2+3y2-3b2=0,
${x_A}^2+3{y_A}^2-3{b^2}=0$,有 b4-4b2+4=0…(10分)
所以b2=2,$\frac{x^2}{6}+\frac{y^2}{2}=1$…(12分)
点评 本题考查椭圆的简单性质与直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
9.从装有两个红球和三个黑球的口袋里任取两个球,那么互斥而不对立的两个事件是( )
| A. | “至少有一个黑球”与“都是黑球” | |
| B. | “至少有一个黑球”与“至少有一个红球” | |
| C. | “恰好有一个黑球”与“恰好有两个黑球” | |
| D. | “至少有一个黑球”与“都是红球” |
6.在各项为正实数的等差数列{an}中,其前2016项的和S2016=1008,则$\frac{1}{{{a_{1001}}}}+\frac{1}{{{a_{1016}}}}$的最小值为( )
| A. | 6 | B. | 4 | C. | $\frac{1}{84}$ | D. | $\frac{1}{251}$ |
3.已知tanα=$\frac{1}{2}$,tanβ=-$\frac{1}{3}$,则$\frac{3sinαcosβ-sinβcosα}{cosαcosβ+2sinαsinβ}$=( )
| A. | $\frac{7}{8}$ | B. | $\frac{11}{8}$ | C. | $\frac{7}{4}$ | D. | $\frac{11}{4}$ |
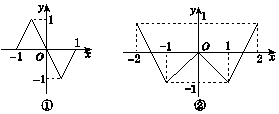 已知奇函数f(x)、偶函数g(x)的图象分别如图①②所示,若方程f[g(x)]=0,g[f(x)]=0的实根个数分别为a,b,则a+b等于( )
已知奇函数f(x)、偶函数g(x)的图象分别如图①②所示,若方程f[g(x)]=0,g[f(x)]=0的实根个数分别为a,b,则a+b等于( )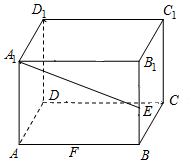 已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点F是AB边上动点,点E是棱B1B的中点.
已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点F是AB边上动点,点E是棱B1B的中点.