题目内容
在△ABC中，a：b：c=1：3：3，求
．
| 2sinA-sinB |
| sinC |
考点：正弦定理
专题：解三角形
分析：直接利用正弦定理，转化角为边的关系，求出结果．
解答：
解：a：b：c=1：3：3，令a=t，则b=c=3t．
由正弦定理可得：
=
=
=-
．
故答案为：-
．
由正弦定理可得：
| 2sinA-sinB |
| sinC |
| 2a-b |
| c |
| 2t-3t |
| 3t |
| 1 |
| 3 |
故答案为：-
| 1 |
| 3 |
点评：本题考查正弦定理的应用，三角形的解法，考查计算能力．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
甲、乙、丙、丁、戊五名应届师范毕业生分配到A，B，C三所学校任教，其中A学校和B学校要2人，C学校要1人，且甲、乙两人不能到同一所学校任教，则不同的分配方案的种数为（ ）
| A、30 | B、48 | C、24 | D、36 |
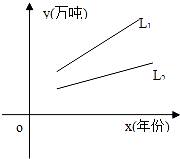对某种产品市场产销量情况如图所示，其中：L1表示产品各年年产量的变化规律；L2表示产品各年的销售情况．下列叙述：