题目内容
(本小题共14分)
设函数![]() (
(![]() ).
).
(Ⅰ)当![]() 时,求
时,求![]() 的极值;
的极值;
(Ⅱ)当![]() 时,求
时,求![]() 的单调区间.
的单调区间.
(共14分)
解:(Ⅰ)依题意,知![]() 的定义域为
的定义域为![]() .
.
当![]() 时,
时,![]() ,
,![]()
![]() .
.
令![]() ,解得
,解得![]() .
.
当![]() 变化时,
变化时,![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
| 0 |
|
|
| 单调递增 | 极大值 | 单调递减 |
由上表知:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故当![]() 时,
时, ![]() 取得极大值为
取得极大值为![]() .-------------------5分
.-------------------5分
(Ⅱ)![]()
![]()
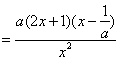
若![]() ,令
,令![]() ,解得:
,解得:![]() ;令
;令![]() ,解得:
,解得:![]() .
.
若![]() ,①当
,①当![]() 时,
时,![]()
令![]() ,解得:
,解得:![]() ;
;
令![]() ,解得:
,解得:![]() 或
或![]() .
.
②当![]() 时,
时,![]() ,
,![]()
③当![]() 时,
时,![]()
令![]() ,解得:
,解得:![]() ;
;
令![]() ,解得:
,解得:![]() 或
或![]() .
.
综上,当![]() 时,
时,![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;
;
当![]() 时,
时,![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,
,![]() ;
;
当![]() 时,
时,![]() 的减区间为
的减区间为![]() ,无增区间;
,无增区间;
当![]() 时,
时,![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,
,![]() .
.
-------------14分

练习册系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是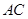 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.