题目内容

F₁，F₂是椭圆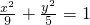 $数学公式$ 的两个焦点，A为椭圆上一点，且∠AF₁F₂=60°，则△AF₁F₂的面积为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

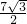
B
分析：求出F₁F₂的长度，由椭圆的定义可得AF₂=6-AF₁，由余弦定理求得AF₁，从而求得三角形AF₁F₂的面积．
解答：由题意可得 a=3，b= $\text{[math]}$ ，c=2，故 F₁F₂=2×2=4，
AF₁+AF₂=6，AF₂=6-AF₁，
∵AF₂²=AF₁²+F₁F₂²-2AF₁•F₁F₂cos60°=AF₁²-4AF₁+16，
∴（6-AF₁）²=AF₁²-4AF₁+16，
∴AF₁= $\text{[math]}$ ，
故三角形AF₁F₂的面积S= $\text{[math]}$ × $\text{[math]}$ ×4× $\text{[math]}$ = $\text{[math]}$ ．
故选B．
点评：本题考查椭圆的定义、标准方程，简单性质，以及余弦定理的应用，求出 AF₁ 的值，是解题的关键．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

点p（x，y）是椭圆

=1（a＞b＞0上的任意一点，F₁、F₂是椭圆的两个焦点，且∠F₁PF₂≤90°，则该椭圆的离心率的取值范围是

已知F₁，F₂是椭圆的两焦点，P为椭圆上一点，若∠F₁PF₂=60°，则离心率e的范围是

已知点P是椭圆

=1上的一点，F₁、F₂是椭圆的两个焦点，∠F₁PF₂=60°，则△F₁PF₂的面积是

=1(a＞b＞0)上有一点M，F₁，F₂是椭圆的两个焦点，若|MF1|•|MF2|=2b2，则椭圆离心率的范围是（　　）

P是椭圆上一定点，F₁，F₂是椭圆的两个焦点，若∠PF₁F₂=60°，∠PF₂F₁=30°，则椭圆的离心率为