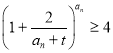题目内容
【题目】已知抛物线![]() 为抛物线的焦点,
为抛物线的焦点,![]() 是过焦点的动弦,
是过焦点的动弦,![]() 是
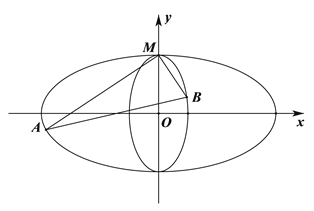
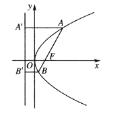
是![]() 两点在准线上的投影,如图所示,则下列论断正确的个数有( )
两点在准线上的投影,如图所示,则下列论断正确的个数有( )
①以![]() 为直径的圆与准线一定相切;
为直径的圆与准线一定相切;
②以![]() 为直径的圆与直线
为直径的圆与直线![]() 一定相切;
一定相切;
③以![]() 为直径的圆与
为直径的圆与![]() 轴一定相切;
轴一定相切;
④以![]() 为直径的圆与
为直径的圆与![]() 轴有可能相切
轴有可能相切
A.1个B.2个C.3个D.4个
【答案】D
【解析】
设![]() ,计算
,计算![]() ,
,![]() 得到①正确;证明
得到①正确;证明![]() ,
,![]() ,计算
,计算![]() 得到②;计算
得到②;计算![]() ,且
,且![]() 轴得到③正确;假设存在,联立方程方程有解得到④正确,得到答案.
轴得到③正确;假设存在,联立方程方程有解得到④正确,得到答案.
设![]() .
.
①如图1,![]() 分别是
分别是![]() 的中点,所以
的中点,所以![]() ,
,
且![]() ,设以
,设以![]() 为直径的圆的半径为
为直径的圆的半径为![]() ,因为
,因为![]() ,
,
所以![]() ,所以以
,所以以![]() 为直径的圆与准线相切;
为直径的圆与准线相切;
②如图2,![]() ,设以
,设以![]() 为直径的圆的半径为
为直径的圆的半径为![]() ,
,
则![]() ,
,![]() ,
,
即![]() ,故
,故![]() ,故
,故
![]() ,
,![]() 是
是![]() 的中点,则
的中点,则![]() ,由①知,
,由①知,![]() ,又
,又![]() ,
,
所以![]() ,所以以
,所以以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切;
相切;
③如图3,设以![]() 为直径的圆的半径为
为直径的圆的半径为![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,
则![]() ,且
,且![]() 轴,
轴,
所以以![]() 为直径的圆与
为直径的圆与![]() 轴相切;
轴相切;
④假设存在以![]() 为直径的圆与
为直径的圆与![]() 轴相切,则有
轴相切,则有![]() ,即
,即![]() ,
,
又![]() ,联立得
,联立得![]() ,
,
![]() 或
或![]() ,故假设成立,
,故假设成立,
因此①②③④都正确,
故选:D.




练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目