题目内容
【题目】现有甲,乙两种不透明充气包装的袋装零食,每袋零食甲随机附赠玩具![]() ,
,![]() ,
,![]() 中的一个,每袋零食乙从玩具
中的一个,每袋零食乙从玩具![]() ,
,![]() 中随机附赠一个.记事件
中随机附赠一个.记事件![]() :一次性购买
:一次性购买![]() 袋零食甲后集齐玩具
袋零食甲后集齐玩具![]() ,
,![]() ,
,![]() ;事件
;事件![]() :一次性购买
:一次性购买![]() 袋零食乙后集齐玩具
袋零食乙后集齐玩具![]() ,
,![]() .
.
(1)求概率![]() ,
,![]() 及
及![]() ;
;
(2)已知![]() ,其中
,其中![]() ,
,![]() 为常数,求
为常数,求![]() .
.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)一次性购买4袋零食甲获得玩具的情况共有![]() 种不同的可能,其中能够集齐三种玩具的充要条件是
种不同的可能,其中能够集齐三种玩具的充要条件是![]() ,
,![]() ,
,![]() 三个玩具中,某个玩具出现两次,其余玩具各出现一次, 计算得到概率,同理可得答案.
三个玩具中,某个玩具出现两次,其余玩具各出现一次, 计算得到概率,同理可得答案.
(2)记![]() ,
,![]() ,计算
,计算![]() ,得到
,得到![]() ,利用累加法计算得到答案.
,利用累加法计算得到答案.
(1)一次性购买4袋零食甲获得玩具的情况共有![]() 种不同的可能,
种不同的可能,
其中能够集齐三种玩具的充要条件是![]() ,
,![]() ,
,![]() 三个玩具中,某个玩具出现两次,其余玩具各出现一次,对应的可能性为
三个玩具中,某个玩具出现两次,其余玩具各出现一次,对应的可能性为![]() ,故
,故![]() ,
,
一次性购买5袋零食甲获得玩具的情况共有![]() 不同的可能,
不同的可能,
其中能够集齐三种玩具的充要条件是![]() ,
,![]() ,
,![]() 三个玩具中,某个玩具出现三次,其余玩具各出现一次或某两个玩具各出现两次,另一个玩具出现一次,对应的可能性分别为
三个玩具中,某个玩具出现三次,其余玩具各出现一次或某两个玩具各出现两次,另一个玩具出现一次,对应的可能性分别为![]() ,
,![]() ,
,
故![]() .
.
一次性购买4袋零食乙获得玩具的情况共有![]() 种不同的可能,
种不同的可能,
其中不能集齐两种玩具的情况只有2种,即全是![]() ,全是
,全是![]() ,故
,故![]() .
.
(2)记![]() ,
,![]() ,根据题意及(1)的计算,不难整理得下表:
,根据题意及(1)的计算,不难整理得下表:
| 1 | 2 | 3 | 4 | 5 |
| 0 | 0 |
|
|
|
| 0 |
|
|
| … |
由于![]() 的对立事件总是2种情形(即全是
的对立事件总是2种情形(即全是![]() ,全是
,全是![]() ),
),
容易得到![]() .
.
为解出待定系数![]() ,
,![]() ,令
,令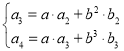 ,即
,即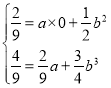 ,
,
解得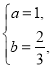 或
或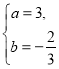 (舍去,因为
(舍去,因为![]() ).
).
故![]() ,即
,即![]() ,
,
同理![]() ,
,
……
![]() ,
,
累加可得![]() (
(![]() ).
).
当![]() 时,
时,![]() 适合上式,∴
适合上式,∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目