题目内容
【题目】已知椭圆![]()
![]() 是椭圆内任一点.设经过
是椭圆内任一点.设经过![]() 的两条不同直线
的两条不同直线![]() 分别于椭圆交于点
分别于椭圆交于点![]() 记
记![]() 的斜率分别为
的斜率分别为![]()
(1)当![]() 经过椭圆右焦点且
经过椭圆右焦点且![]() 为
为![]() 中点时,求:
中点时,求:
①椭圆![]() 的标准方程;
的标准方程;
②四边形![]() 面积
面积![]() 的取值范围.
的取值范围.
(2)当![]() 时,若点
时,若点![]() 重合于点
重合于点![]()
![]() ,且
,且![]() .求证:直线
.求证:直线![]() 过定点
过定点![]() .
.
【答案】(1) ①![]() ;②
;②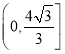 ;(2)见解析.
;(2)见解析.
【解析】
(1) ①由方程可求出焦点坐标,进而可求![]() 的斜率.设出
的斜率.设出![]() ,将
,将![]() 代入到椭圆方程中去,将所得方程相减整理,
代入到椭圆方程中去,将所得方程相减整理, ![]() ,结合中点坐标和
,结合中点坐标和![]() 的斜率可求
的斜率可求![]() .
.
②由分析知, 当过![]() 点与
点与![]() 的直线同时和椭圆相切时四边形
的直线同时和椭圆相切时四边形![]() 的面积最大. 设切线方程为
的面积最大. 设切线方程为![]() ,与椭圆联立整理后令
,与椭圆联立整理后令![]() ,即可求出切点
,即可求出切点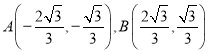 ,进而可求切点到直线
,进而可求切点到直线![]() 的距离
的距离![]() ,由弦长公式求出
,由弦长公式求出![]() 的长度,进而可求四边形的面积.
的长度,进而可求四边形的面积.
(2)设出![]() 的方程,与椭圆联立,得到
的方程,与椭圆联立,得到![]() 横坐标的关系,由
横坐标的关系,由![]() ,可求出
,可求出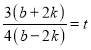 ,进而可知
,进而可知![]() .因此可证过定点.
.因此可证过定点.
(1) ①解:由题意知,![]() .即椭圆的焦点坐标为
.即椭圆的焦点坐标为![]() .
.
则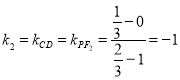 .设
.设![]()
则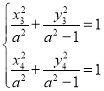 两式相减整理得
两式相减整理得![]()
![]() 是
是![]() 的中点,
的中点,![]() 解得
解得![]()
故椭圆的方程为![]() .
.
②解:由题意知,当过![]() 点与
点与![]() 的直线同时和椭圆相切时四边形
的直线同时和椭圆相切时四边形![]() 的面积最大.
的面积最大.
由![]() 知,切线斜率也为
知,切线斜率也为![]() .设切线方程为
.设切线方程为![]() ,与椭圆联立得
,与椭圆联立得
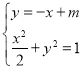 ,整理得
,整理得![]() ,则
,则
![]() ,解得
,解得![]() .
.
则可求切点不妨设为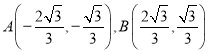 ,此时两点到
,此时两点到![]() 的距离
的距离
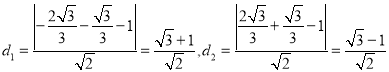
设![]() ,联立
,联立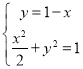 ,整理得
,整理得![]() ,则
,则
由韦达定理知![]() .
.
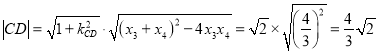
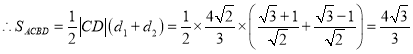
故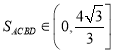 .
.
(2)证明:当![]() 时,椭圆的方程为
时,椭圆的方程为![]() .
.
![]()
![]() 直线
直线![]() 的斜率存在且不为0,直线
的斜率存在且不为0,直线![]() 不过
不过![]()
设直线![]() 的方程为
的方程为![]() ,
,![]() 此时
此时![]()
联立得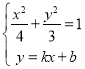 ,整理得
,整理得![]()
则![]() .
.![]()

即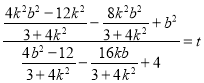 整理得
整理得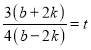
解得![]() 此时
此时![]()
故直线![]() 恒过
恒过![]() .
.

 走进文言文系列答案
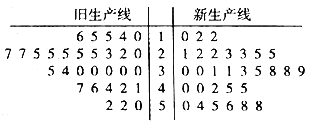
走进文言文系列答案【题目】近几年,我国鲜切花产业得到了快速发展,相关部门制定了鲜切花产品行业等级标准,统一使用综合指标值![]() 进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
综合指标 |
|
|
|
质量等级 | 三级 | 二级 | 一级 |
(Ⅰ)根据茎叶图比较两条生产线加工的产品的综合指标值的平均值及分散程度(直接给出结论即可);
(Ⅱ)若从等级为三级的样品中随机选取3个进行生产流程调查,其中来自新型生产线的样品个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)根据该花卉生产基地的生产记录,原有生产线加工的产品的单件平均利润为4元,产品的销售率(某等级产品的销量与产量的比值)及产品售价如下表:
三级花 | 二级花 | 一级花 | |
销售率 |
|
|
|
单件售价 | 12元 | 16元 | 20元 |
预计该新型生产线加工的鲜切花单件产品的成本为span>10元,日产量3000件.因为鲜切花产品的保鲜特点,未售出的产品统一按原售价的50%全部处理完.如果仅从单件产品利润的角度考虑,该生产基地是否需要引进该新型生产线?