题目内容
求数列{n(n+1)(n+2)}的前n项和.
分析:设ak=k(k+1)(2k+1)=2k3+3k2+k,故Sn=
k(k+1)(2k+1)=
(2k3+3k2+k),将其每一项拆开再重新组合得:Sn=2
k3+3
k2+
k,由此能求出数列{n(n+1)(n+2)}的前n项和.
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| n |
 |
| k=1 |
解答:解:设ak=k(k+1)(2k+1)=2k3+3k2+k,
∴Sn=
k(k+1)(2k+1)=
(2k3+3k2+k),
将其每一项拆开再重新组合得:
Sn=2
k3+3
k2+
k
=2(13+23+…+n3)+3(12+22+…+n2)+(1+2+…+n)
=
+
+
=
.
∴Sn=
| n |
 |
| k=1 |
| n |
 |
| k=1 |
将其每一项拆开再重新组合得:
Sn=2
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| n |
 |
| k=1 |
=2(13+23+…+n3)+3(12+22+…+n2)+(1+2+…+n)
=
| n2(n+1)2 |
| 2 |
| n(n+1)(2n+1) |
| 2 |
| n(n+1) |
| 2 |
=
| n(n+1)2(n+2) |
| 2 |
点评:本题考查数列求和的方法,是中档题.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 已知数列{an}满足如图所示的流程图
已知数列{an}满足如图所示的流程图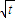 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点 ,数列{bn}前n项的和为Sn,求证:Sn
,数列{bn}前n项的和为Sn,求证:Sn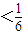
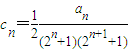 ,数列{cn}前n项的和为Tn,求同时满足下列两个条件的t的值:
,数列{cn}前n项的和为Tn,求同时满足下列两个条件的t的值: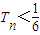
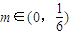 ,均存在k∈N*,当n≥k时,Tn>m.
,均存在k∈N*,当n≥k时,Tn>m.