题目内容
(理)已知函数f(x)=
(0＜x＜1)的反函数为f-1(x)，设它在点(n,f-1(n))(n∈N*)处的切线在Y轴上的截距为bn，数列{an}满足：a1=2，an+1=f-1(an)(n∈N*)．
(1)求数列{an}的通项公式；
(2)在数列{
}中，仅当n=5时，
取最小值，求A的取值范围；
(3)令函数g(x)=f-1(x)(1+x)2，数列{cn}满足：c1=
，cn+1=g(cn)(n∈N*)，求证：对于一切
n≥2的正整数，都满足：1＜
＜2．
(文)已知函数f(x)：
(0＜x＜1)的反函数为f-1(x)，数列{an}满足：a1=2，an+1=f-1(an) (n∈N*)．
(1)求数列{an}的通项公式；
(2)设函数g(x)=f-1(x)(1+x)2在点(n，g(n))(n∈N*)处的切线在Y轴上的截距为bn，求数列{bn}的通项公式；
(3)在数列{bn+
}中，仅当n=5时，bn+
取最大值，求λ的取值范围．
答案：(理)(1)∵f(x)=,
∴函数f(x)=(0＜x＜1)的反函数为
f-1(x)=(x＞0)．
则an+1=f-1(an)=,
得+1，即=1，
∴数列{}是以2为首项、1为公差的等差数列，故an=.
(2)又∵[f-1(x)]′=
.
∴函数f-1(x)在点(n，f-1(n))(n∈N*)处的切线方程为：y-f-1(n)=
(x-n)，
令x=0，得bn=
∴
=n2+λ(n+1)=(n+
)2+λ
,
仅当n=5时取最小值，只需4.5＜
＜5.5，解得-11＜λ＜-9．
故A的取值范围为(-11，-9)．
(3)∵g(x)=f-1(x)(1+x)2=x(1+x)，
故cn+1=g(cn)=cn(1+cn)，
又∵c1=
＞0，故cn＞0，
则
,
即
,
∴
=(
)+(
)+…+(
)
=
,
又
＞
=
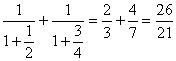＞1,
故1＜
+…+
＜2.
(文)(1)∵f(x)=
,
∴函数f(x)=
(0＜x＜1)的反函数为f-1(x)=
(x＞0)．
贝an+1=f-1(an)=
，得
+1，即
=1，
∴数列{
}是以2为首项、1为公差的等差数列，故an=
.
(2)∵g(x)=f-1(x)(1+x)2=
(1+x)2=x+x2，
∴g′(x)=1+2x，即在点(n，g(n))处切线的斜率k=g′(n)=1+2n，
∴切线方程为y-g(n)=(1+2n)(x-n)，
令x=0，得bn=g(n)-n-2n2=-n2．
(3)bn+
=-n2+λ(n+1)=-(n
)2+λ+
仅在n=5时取最大值，只需4.5＜
＜5.5，解得9＜λ＜11．
故λ的取值范围为(9，11)．
口算题卡加应用题集训系列答案
综合自测系列答案
（理）已知函数
（2011•普陀区三模）（理）已知函数