题目内容
1.已知命题p:?x∈N*,2x>x2,则¬p是( )| A. | ?x∈N*,2x>x2 | B. | ?x∈N*,2x≤x2 | C. | ?x∈N*,2x≤x2 | D. | ?x∈N*,2x<x2 |
分析 欲写出命题的否定,必须同时改变两个地方:①:“?”;②:“>”即可,据此分析选项可得答案.
解答 解:命题p:?x∈N*,2x>x2,则¬p是?x∈N*,2x≤x2,
故选:C.
点评 这类问题的常见错误是没有把全称量词改为存在量词,或者对于“>”的否定用“<”了.这里就有注意量词的否定形式.如“都是”的否定是“不都是”,而不是“都不是”.特称命题的否定是全称命题,“存在”对应“任意”.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
15.若cos(π-α)=-$\frac{\sqrt{3}}{3}$,则cosα=( )
| A. | -$\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
16.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,P为双曲线C上一点,Q为双曲线C渐近线上一点,P,Q均位于第一象限,且$\widehat{QP}$=$\widehat{P{F}_{2}}$,$\widehat{Q{F}_{1}}$•$\widehat{Q{F}_{2}}$=0,则双曲线C的离心率为( )
| A. | $\sqrt{5}$-1 | B. | $\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | $\sqrt{5}$+1 |
6.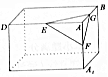 如图,用小刀切一块长方体橡皮的一个角,在棱AD、AA1、AB上的截点分别是E、F、G,则截面△EFG( )
如图,用小刀切一块长方体橡皮的一个角,在棱AD、AA1、AB上的截点分别是E、F、G,则截面△EFG( )
 如图,用小刀切一块长方体橡皮的一个角,在棱AD、AA1、AB上的截点分别是E、F、G,则截面△EFG( )
如图,用小刀切一块长方体橡皮的一个角,在棱AD、AA1、AB上的截点分别是E、F、G,则截面△EFG( )| A. | 一定是等边三角形 | B. | 一定是钝角三角形 | ||
| C. | 一定是锐角三角形 | D. | 一定是直角三角形 |
10.若函数f(x)=a(x2+$\frac{2}{x}$)-lnx(a>0)有唯一零点x0,且m<x0<n(m,n为相邻整数),其中自然对数e=2.71828…,则m+n的值为( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
11.在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上,若圆C上存在点M,使|MA|=2|MO|,则圆心C的横坐标的取值范围为( )
| A. | $[{0,\frac{12}{5}}]$ | B. | [0,1] | C. | $[{1,\frac{12}{5}}]$ | D. | $({0,\frac{12}{5}})$ |