题目内容
若数列 满足①
满足① ,②存在常数
,②存在常数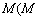 与
与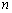 无关),使
无关),使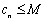 .则称数列
.则称数列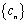 是“和谐数列”.
是“和谐数列”.
(1)设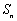 为等比数列
为等比数列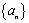 的前
的前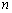 项和,且
项和,且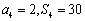 ,求证:数列
,求证:数列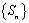 是“和谐数列”;
是“和谐数列”;
(2)设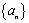 是各项为正数,公比为q的等比数列,
是各项为正数,公比为q的等比数列,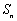 是
是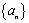 的前
的前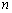 项和,求证:数列
项和,求证:数列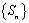 是“和谐数列”的充要条件为
是“和谐数列”的充要条件为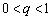 .
.
(1)设公比为 ,则
,则 ,
,
所以 .
.
因为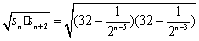
=

= .
.
且 即存在常数32,
即存在常数32,
所以,数列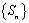 是“和谐数列” .
是“和谐数列” .
(2)充分性
设等比数列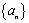 的公比
的公比 ,且
,且
则 .
.
令 ,则
,则
因为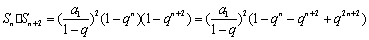

所以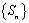 是“和谐数列”
是“和谐数列”
必要性
等比数列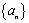 各项为正,且
各项为正,且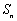 是“和谐数列”.
是“和谐数列”.
因为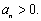 所以,
所以,
下面用反证法证明,
(1)当 则
则 因为
因为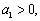 所以,不存在
所以,不存在 ,使
,使 对
对 恒成立;
恒成立;
当 ,则
,则
所以,对于给定的正数 ,若
,若
因为, ,所以,
,所以,
即当 时,有
时,有 .
.
所以,不存在常数 ,使
,使
所以,
综上,数列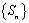 是“和谐数列”的充要条件为其公比为
是“和谐数列”的充要条件为其公比为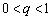 .
.

练习册系列答案
相关题目
 ,
, .若
.若 ,则实数
,则实数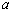 的取值范围是 .
的取值范围是 .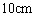 的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为
的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为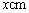 ,体积为
,体积为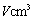 .
.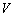 关于
关于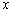 的函数关系式;
的函数关系式;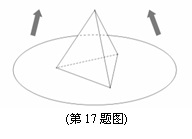
 中,已知
中,已知 ,那么满足
,那么满足 的
的 平面上,点
平面上,点 ,点
,点 在单位圆上,
在单位圆上, (
( )
) ,求
,求 的值;
的值; ,
, ,求
,求 .
.
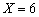 的概率;
的概率; 的右准线为准线的抛物线方程是 .
的右准线为准线的抛物线方程是 . 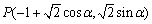 (其中
(其中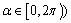 ,点
,点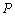 的轨迹记为曲线
的轨迹记为曲线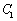 ,以坐标原点为极点,
,以坐标原点为极点,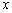 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点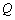 在曲线
在曲线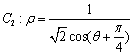 上.
上.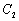 的直角坐标方程;
的直角坐标方程;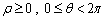 时,求曲线
时,求曲线 中,角A,B,C的对边分别为a,b,c,且
中,角A,B,C的对边分别为a,b,c,且 若
若 ,则
,则 的最小值为_________.
的最小值为_________.