题目内容
19.若集合A={(x,y)|y=-$\sqrt{9-{x}^{2}}$},B={(x,y)|x+y+m=0},且A∩B≠∅,则实数m的取值范围[-3,3$\sqrt{2}$].分析 根据集合的关系,转化为直线和曲线的相交问题进行求解即可.
解答  解:∵A∩B≠∅,
解:∵A∩B≠∅,
∴直线x+y+m=0与y=-$\sqrt{9-{x}^{2}}$有交点,
作出y=-$\sqrt{9-{x}^{2}}$对应的图象是以原点为圆心,半径r=3的圆的下部分,
当直线x+y+m=0经过点(3,0)时,此时3+m=0,得m=-3,
当直线x+y+m=0在第三象限与圆相切时,
此时直线方程为y=-x-m,
直线截距-m<0,则m>0,
圆心到直线的距离d=$\frac{|m|}{\sqrt{2}}$=3,
即|m|=3$\sqrt{2}$,解得m=3$\sqrt{2}$或m=-3$\sqrt{2}$(舍),
∴若直线和曲线有公共点,则-3≤m≤3$\sqrt{2}$,
故答案为:[-3,3$\sqrt{2}$].
点评 本题主要考查集合关系的应用,根据条件转化为直线和曲线的相交问题是解决本题的关键.

练习册系列答案
相关题目
10.若图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则这个几何体外接球的表面积为( )
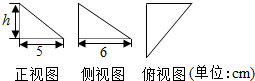

| A. | 25xcm2 | B. | $\frac{77π}{2}$cm2 | C. | 77πcm2 | D. | 144πcm2 |
13.设x>0,则“a=1”是“x+$\frac{a}{x}$≥2恒成立”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
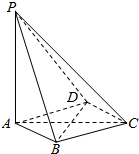 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.