题目内容
如图,在棱长为a的正方体OABC-O1A1B1C1中,E、F分别是棱AB、BC上的动点,且AE=BF=x,其中0≤x≤a,以O为原点建立空间直角坐标系O-xyz.
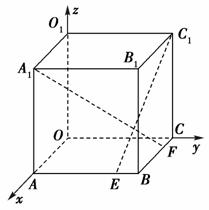
(1)写出点E、F的坐标;
(2)求证:A1F⊥C1E;
(3)若A1、E、F、C1四点共面,求证: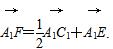
[解析] (1)解:E(a,x,0),F(a-x,a,0).
 即(-x,a,-a)=λ1(-a,a,0)+λ2(0,x,-a)
即(-x,a,-a)=λ1(-a,a,0)+λ2(0,x,-a)
=(-aλ1,aλ1+xλ2,-aλ2),


练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
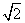 的圆C与直线y=x相切于坐标原点O.
的圆C与直线y=x相切于坐标原点O.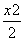 +y2=1 B.
+y2=1 B.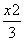 +
+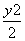 =1
=1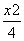 +
+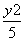 =1 D.
=1 D.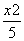 +
+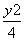 =1
=1 ,N为B1B的中点,则|
,N为B1B的中点,则| |为( )
|为( ) a B.
a B. a
a  a D.
a D. a
a ,则cos
,则cos 的值为( )
的值为( )
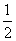
 D.
D.

