Question

已知函数f（x）=

2x

x2+a

的图象如图所示．
（1）求a的值；
（2）写出f（x）的单调递增区间，并解方程：f（sinα）+f（cosα）=0；
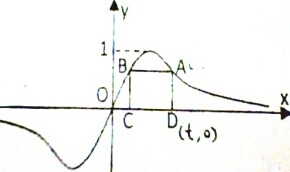
（3）矩形ABCD的两个顶点A、B在函数f（x）的图象上（位于第一象限，且点A在点B右侧），另两个顶点C、D在x轴上，设顶点A的横坐标为t，试用t表示矩形ABCD面积S，并求矩形ABCD面积S的取值范围．

Answer 1

考点：函数最值的应用

专题：压轴题

分析：（1）求函数的导数，利用导数研究函数的单调性，利用函数的最大值为1来求a
 （2）利用f（x）为奇函数，把f（sinα）+f（cosα）=0等价转化为f（sinα）=f（-cosα），再应用单调性求解．
（3）先求C点的横坐标，然后表示四边形的面积S，建立S是t的函数，利用求函数的值域求面积的范围

解答： 解：（1）易求f′（x）=

-2(x2-a)

(x2+a)2

若-a≥0，则x²-a≥0，则f′（x）≥0，函数f（x）单调，这与已知函数不单调相矛盾，故-a＜0，∴a＞0，
令f′（x）=0得x=-

a

、x=

a

．
∴在（-∞，-

a

）时f′（x）＜0、在（-

a

，

a

）时f′（x）＞0、在（

a

，+∞）时f′（x）＜0，
∴函数f（x）在（-∞，-

a

）时递减、在[-

a

，

a

]时递增、在（

a

，+∞）时递减
∴x＞0时，当x=

a

时f（x）取最大值f（

a

），∴f（

a

）=1，∴

2 a

( a )2+a

=1，解得a=1．
（2）由第（1）问知，a=1，∴f（x）=

2x

x2+1

，且f（x）在[-

a

，

a

]也即在[-1，1]时递增，
易知函数f（x）为奇函数，∴f（sinα）+f（cosα）=0?f（sinα）=-f（cosα）?f（sinα）=f（-cosα），
又f（x）在[-1，1]时单调递增，故sinα=-cosα，∴tanα=-1
∴α=kπ-

π

4

，（k∈Z）
（3）易知t＞1，设C的横坐标为m，则f（m）=f（t），∴

2m

m2+1

=

2t

t2+1

，
整理得（t-m）（mt-1）=0，由于m≠t，∴mt-1=0，∴m=

1

t

，
矩形ABCD的长为t-

1

t

，宽为f（t）=

2t

t2+1

∴S=（t-

1

t

）

2t

t2+1

，
∴S=（t-

1

t

）

2t

t2+1

=

2t2-2

t2+1

=2-

4

t2+1

．
∵t＞1，∴t²＞1，∴t²+1＞2，∴2-

4

t2+1

∈（0，2），
∴矩形ABCD面积S的取值范围为（0，2）．

点评：本题主要考查函数与导数的综合应用、函数单调性的判断与证明．解本题的关键是灵活应用题目条件，尤其是从图中函数的单调性判断出a＞0是关键，这里体现了向条件探究的策略．