题目内容
19.已知在△ABC中,角A,B,C所对的边分别为a,b,c,若$\overrightarrow{BA}$•$\overrightarrow{BC}$=$\frac{3\sqrt{3}}{2}$,$\sqrt{3}$bsinA=acosB,a+c=4.(1)求a,c.
(2)求角B的平分线BD的长.
分析 (1)运用向量的数量积的定义,结合正弦定理,即可得到所求a,c的值;
(2)运用内角平分线定理,可得$\overrightarrow{BD}$=$\frac{1}{4}$($\overrightarrow{BA}$+3$\overrightarrow{BC}$)或$\frac{1}{4}$(3$\overrightarrow{BA}$+$\overrightarrow{BC}$),再由向量的平方即为模的平方,计算即可的所求值.
解答 解:(1)由$\overrightarrow{BA}$•$\overrightarrow{BC}$=$\frac{3\sqrt{3}}{2}$,可得accosB=$\frac{3\sqrt{3}}{2}$,
$\sqrt{3}$bsinA=acosB,可得$\sqrt{3}$sinBsinA=sinAcosB,
即有tanB=$\frac{sinB}{cosB}$=$\frac{\sqrt{3}}{3}$,解得B=30°,
ac=3,又a+c=4,
可得a=1,c=3,或a=3,c=1;
(2)若a=1,c=3,可得$\frac{AD}{DC}$=$\frac{AB}{CB}$=3,
即有$\overrightarrow{BD}$=$\frac{\overrightarrow{BA}+3\overrightarrow{BC}}{1+3}$=$\frac{1}{4}$($\overrightarrow{BA}$+3$\overrightarrow{BC}$),
可得$\overrightarrow{BD}$2=$\frac{1}{16}$($\overrightarrow{BA}$+3$\overrightarrow{BC}$)2=$\frac{1}{16}$(c2+9a2+6$\overrightarrow{BA}$•$\overrightarrow{BC}$)
=$\frac{1}{16}$(9+9+9$\sqrt{3}$)=$\frac{18+9\sqrt{3}}{16}$,
即有角B的平分线BD的长为$\frac{3}{8}$($\sqrt{6}$+$\sqrt{2}$);
若a=3,c=1,可得$\frac{AD}{DC}$=$\frac{AB}{CB}$=$\frac{1}{3}$,
即有$\overrightarrow{BD}$=$\frac{\overrightarrow{BC}+3\overrightarrow{BA}}{1+3}$=$\frac{1}{4}$(3$\overrightarrow{BA}$+$\overrightarrow{BC}$),
可得$\overrightarrow{BD}$2=$\frac{1}{16}$(3$\overrightarrow{BA}$+$\overrightarrow{BC}$)2=$\frac{1}{16}$(9c2+a2+6$\overrightarrow{BA}$•$\overrightarrow{BC}$)
=$\frac{1}{16}$(9+9+9$\sqrt{3}$)=$\frac{18+9\sqrt{3}}{16}$,
即有角B的平分线BD的长为$\frac{3}{8}$($\sqrt{6}$+$\sqrt{2}$).
综上可得角B的平分线BD的长为$\frac{3}{8}$($\sqrt{6}$+$\sqrt{2}$).
点评 本题考查向量的数量积的定义和性质,考查正弦定理的运用,同时考查内角平方线性质定理的运用,考查运算能力,属于中档题.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案| A. | sin$\frac{α}{2}$ | B. | cos$\frac{α}{2}$ | C. | -sin$\frac{α}{2}$ | D. | -cos$\frac{α}{2}$ |
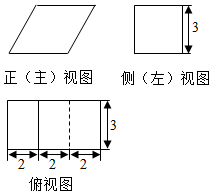
| A. | 48+6$\sqrt{13}$ | B. | 78 | C. | 24+6$\sqrt{13}$ | D. | 68 |