题目内容
19．有下列命题：①若$\overrightarrow{p}$与$\overrightarrow{a}$，b共面，则$\overrightarrow{p}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$（x，y∈R）；
②若$\overrightarrow{p}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$（x，y∈R），则$\overrightarrow{p}$与$\overrightarrow{a}$，$\overrightarrow{b}$共面；
③若$\overrightarrow{a}$、$\overrightarrow{b}$共线，则$\overrightarrow{a}$与$\overrightarrow{b}$所在直线平行；
④对空间任意一点O与不共线的三点A、B、C，若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$ （其中x、y、z∈R），则P、A、B、C四点共面．
其中正确的命题为（ ）
| A． | ① | B． | ② | C． | ③ | D． | ④ |
分析 举例说明①③④错误；由平面向量基本定理说明②正确．
解答 
解：①若$\overrightarrow{p}$与$\overrightarrow{a}$，$\overrightarrow{b}$共面，则$\overrightarrow{p}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$（x，y∈R）不一定成立，如$\overrightarrow{a}=\overrightarrow{b}=\overrightarrow{0}$，而$\overrightarrow{p}≠\overrightarrow{0}$．①错误；
②若$\overrightarrow{p}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$（x，y∈R），则由平面向量基本定理得$\overrightarrow{p}$与$\overrightarrow{a}$，$\overrightarrow{b}$共面．②正确；
③若$\overrightarrow{a}$、$\overrightarrow{b}$共线，则$\overrightarrow{a}$与$\overrightarrow{b}$所在直线平行不正确，可能在同一条直线上；故错
④对空间任意一点O与不共线的三点A、B、C，
如图所示平行六面体，$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$满足条件，但是P、A、B、C四点不共面．④错误．
故选：B．
点评 本题考查命题的真假判断与应用，考查了平面向量的基本概念，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
10．已知某几何体的三视图的侧视图是一个正三角形，如图所示，则该几何体的体积等于（ ）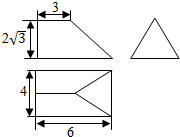
| A． | 12$\sqrt{3}$ | B． | 16$\sqrt{3}$ | C． | 20$\sqrt{3}$ | D． | 32$\sqrt{3}$ |
7．函数f（x）=Asin（ωx+$\frac{π}{6}$）（A＞0，ω＞0）的图象与x轴的交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列，要得到函数g（x）=Acosωx的图象，只需将f（x）的图象（ ）
| A． | 向左平移$\frac{π}{6}$个单位 | B． | 向右平移$\frac{π}{3}$个单位 | ||
| C． | 向左平移$\frac{2π}{3}$个单位 | D． | 向右平移$\frac{2π}{3}$个单位 |