题目内容
13.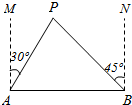 如图,A、B两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上,已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?
如图,A、B两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上,已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?
分析 过点P作PD⊥AB,D是垂足.AD与BD都可以根据三角函数用PD表示出来.根据AB的长,得到一个关于PD的方程,解出PD的长.从而判断出这条高速公路会不会穿越保护区.
解答 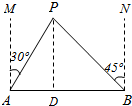 解:过P作PD⊥AB于D,设PD=x,
解:过P作PD⊥AB于D,设PD=x,
在Rt△APD,∠APD=30°,则$AD=x•tan30°=\frac{{\sqrt{3}}}{3}x$.
在Rt△BPD,∠BPD=45°,∴BD=PD=x,
∵AB=100,∴$\frac{{\sqrt{3}}}{3}x+x=100$,
∴$x=({150-50\sqrt{3}})$米>50米.
∴不会穿过保护区.
点评 本题主要考查解直角三角形的应用,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
3.执行如图的框图,若输出结果为2,则输入的实数x的值是( )
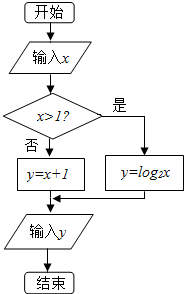

| A. | $\frac{3}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 4 |
4.如图是某算法的程序框图,若输出的b值为32,则判断框内①应填( )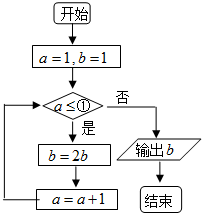

| A. | 4? | B. | 5? | C. | 6? | D. | 7? |
1.已知等差数列{an}前四项中第二项为606,前四项和Sn为2600,则第4项为( )
| A. | 707 | B. | 782 | C. | 870 | D. | 990 |
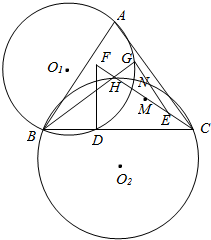 H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:
H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明: