题目内容
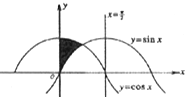 如图,在由x=0,y=0,x=
如图,在由x=0,y=0,x=| π |
| 2 |
A、1-
| ||||
B、
| ||||
C、
| ||||
D、3-2
|
分析:根据积分的几何意义求出阴影部分的面积,利用几何概型的概率公式即可得到结论.
解答:解:由x=0,y=0,x=
及y=cosx围成区域内围成的区域面积S=
cosxdx=sinx|
=sin
=1,
由x=0,y=sinx及y=cosx围成的区域面积S=
(cosx-sinx)dx=(sinx+cosx)|
=
+
-1=
-1,
∴根据根据几何概型的概率公式可得所求的概率P=
=
-1,
故选:B.
| π |
| 2 |
| ∫ |
0 |
0 |
| π |
| 2 |
由x=0,y=sinx及y=cosx围成的区域面积S=
| ∫ |
0 |
0 |
| ||
| 2 |
| ||
| 2 |
| 2 |
∴根据根据几何概型的概率公式可得所求的概率P=
| ||
| 1 |
| 2 |
故选:B.
点评:本题主要考查几何概型的概率计算,利用积分的几何意义求出对应的区域面积是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
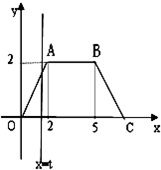 如图,在等腰梯形OABC中,A(2,2),B(5,2).直线x=t(t>0)由点O向点C移动,至点C完毕,记扫描梯形时所得直线x=t左侧的图形面积为f(t).试求f(t)的解析式,并画出y=f(t)的图象.
如图,在等腰梯形OABC中,A(2,2),B(5,2).直线x=t(t>0)由点O向点C移动,至点C完毕,记扫描梯形时所得直线x=t左侧的图形面积为f(t).试求f(t)的解析式,并画出y=f(t)的图象.
 (2013•嘉定区一模)如图,在平面直角坐标系xOy中,椭圆
(2013•嘉定区一模)如图,在平面直角坐标系xOy中,椭圆 如图,一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后再按图所示与x轴、y轴平行的方向运动,且每秒移动一个单位长度,那么经过2000秒后,这个质点所处的位置的坐标是( )
如图,一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后再按图所示与x轴、y轴平行的方向运动,且每秒移动一个单位长度,那么经过2000秒后,这个质点所处的位置的坐标是( )