Question

如图1，已知抛物线C：y=3x²（x≥0）与直线x=a．直线x=b（其中0≤a≤b）及x轴围成的曲边梯形（阴影部分）的面积可以由公式S=b³-a³来计算，则如图2，过抛物线C：y=3x²（x≥0）上一点A（点A在y轴和直线x=2之间）的切线为l，S₁是抛物线y=3x²与切线l及直线y=0所围成图形的面积，S₂是抛物线y=3x²与切线l及直线x=2所围成图形的面积，求面积s₁+s₂的最小值．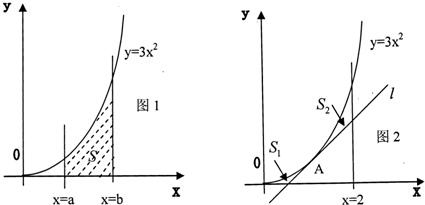

Answer 1

分析：设切点A的坐标为（a，3a²），切线l的方程为y-3a²=6a（x-a），令y=0得x=

a

2

，令x=2得y=12a-3a²，所以S1+S2=23-03-

1

2

(2-

a

2

)(12a-3a2)=-

3

4

a3+6a2-12a+8，记f(a)=-

3

4

a3+6a2-12a+8，转化为求f(a)=-

3

4

a3+6a2-12a+8在a∈[0，2]时的最小值．

解答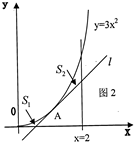：解：设切点A的坐标为（a，3a²），（1分）
则y′|_x=a=6a所以切线l的方程为：
y-3a²=6a（x-a），令y=0
得x=

a

2

，令x=2得y=12a-3a²，（3分）
所以S1+S2=23-03-

1

2

(2-

a

2

)(12a-3a2)=-

3

4

a3+6a2-12a+8，
记f(a)=-

3

4

a3+6a2-12a+8，（5分）
则转化为求f(a)=-

3

4

a3+6a2-12a+8在a∈[0，2]时的最小值，
因为f′(a)=-

9

4

a2+12a-12，由-

9

4

a2+12a-12=0（7分）
解得a=

4

3

或a=4，因为f（0）=8，f（2）=2，f(

4

3

) =

8

9

．（9分）
所以当a=

4

3

，f（a）取得最小值

8

9

．因此面积S₁+S₂的最小值

8

9

．

点评：本题主要考查直线与圆锥曲线的综合应用能力，具体涉及到面积s₁+s₂的最小值的求法及直线与抛物线的相关知识，解题时要注意合理地进行等价转化．