Question

【题目】设f（x）= ，曲线y=f（x）在点（1，f（1））处的切线与直线x+y+1=0垂直． （Ⅰ）求a的值；
（Ⅱ）若对于任意的x∈[1，+∞），f（x）≤m（x﹣1）恒成立，求m的取值范围；
（Ⅲ）求证：ln（4n+1）≤16 （n∈N*）．

Answer 1

【答案】解：（Ⅰ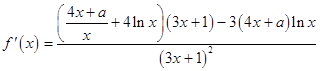） 由题设f'（1）=1，∴ ，即a=0；
（Ⅱ）解： ，x∈[1，+∞），f（x）≤m（x﹣1），即 ，
设 ，即x∈[1，+∞），g（x）≤0．
，g'（1）=4﹣4m．
② 若m≤0，g'（x）＞0，g（x）≥g（1）=0，这与题设g（x）≤0矛盾；
②若m∈（0，1），当 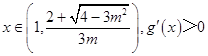，g（x）单调递增，g（x）＞g（1）=0，与题设矛盾；
③若m≥1，当x∈（1，+∞），g'（x）≤0，g（x）单调递减，g（x）≤g（1）=0，即不等式成立；
综上所述，m≥1．
（Ⅲ）证明：由（Ⅱ）知，当x＞1时，m=1时， 成立．
不妨令 ，
∴ ，
即 ， ， ，…， ．
累加可得：ln（4n+1）≤16 （n∈N*）
【解析】（Ⅰ）求出原函数的导函数，结合f'（1）=1列式求得a值；（Ⅱ）把（Ⅰ）中求得的a值代入函数解析式，由f（x）≤m（x﹣1）得到 ，构造函数 ，即x∈[1，+∞），g（x）≤0．然后对m分类讨论求导求得m的取值范围；（Ⅲ）由（Ⅱ）知，当x＞1时，m=1时， 成立．令 ，然后分别取i=1，2，…，n，利用累加法即可证明结论．
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案，需要熟知求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值．