题目内容
【题目】在平面内,定点A,B,C,D满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,|
|,| ![]() ||
|| ![]() |=|
|=| ![]() ||
|| ![]() |=|
|=| ![]() ||
|| ![]() |=﹣4,动点P,M满足|
|=﹣4,动点P,M满足| ![]() |=2,
|=2, ![]() =
= ![]() ,则|
,则| ![]() |的最大值是 .
|的最大值是 .
【答案】3 ![]() +1
+1
【解析】解:∵| ![]() |=|
|=| ![]() |=|
|=| ![]() |,∴A,B,C在以D为圆心的圆D上,
|,∴A,B,C在以D为圆心的圆D上,
∵ ![]()
![]() =
= ![]() =
= ![]()
![]() =﹣4,∴
=﹣4,∴ ![]() 两两夹角相等均为120°,∴|DA|=2
两两夹角相等均为120°,∴|DA|=2 ![]() ,
,
以D为原点建立平面直角坐标系,设A(2 ![]() ,0),则B(﹣
,0),则B(﹣ ![]() ,﹣
,﹣ ![]() ),C(﹣
),C(﹣ ![]() ,
, ![]() ),
),
∴ ![]() =(0,2
=(0,2 ![]() ).
).
∵| ![]() |=2,∴P在以A为圆心,以2为半径的圆A上,
|=2,∴P在以A为圆心,以2为半径的圆A上,
∵ ![]() =
= ![]() ,∴M为PC的中点,∴
,∴M为PC的中点,∴ ![]() =
= ![]() (
( ![]() ).
).
设P(2 ![]() +2cosα,2sinα),则
+2cosα,2sinα),则 ![]() =(3
=(3 ![]() +2cosα,2sinα+
+2cosα,2sinα+ ![]() ),
),
∴ ![]() =
= ![]() (
( ![]() )=(cosα+
)=(cosα+ ![]() ,sinα+
,sinα+ ![]() ),
),
∴ ![]() =(cosα+
=(cosα+ ![]() )2+(sinα+
)2+(sinα+ ![]() )2=3
)2=3 ![]() cosα+3
cosα+3 ![]() sinα+19=6
sinα+19=6 ![]() sin(α+
sin(α+ ![]() )+19,
)+19,
∴| ![]() |的最大值为
|的最大值为 ![]() =
= ![]() =3
=3 ![]() +1.
+1.
所以答案是:3 ![]() +1
+1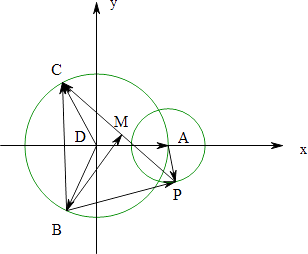

练习册系列答案
相关题目