题目内容
14.若一个三角形两内角α、β满足2α+β=π,则y=cosβ-6sinα的范围为(-5,-1).分析 先由:2α+β=π,结合配方法将y=cos(π-2α)-6siα转化为:y=2(sinα-$\frac{3}{2}$)2-$\frac{11}{2}$,再令t=sinα∈(0,1),用二次函数的性质求解.
解答 解:∵一个三角形两内角α、β满足2α+β=π,∴α、β均大于零,∴2α<π,∴α∈(0,$\frac{π}{2}$).
则y=cosβ-6sinα=cos(π-2α)-6sinα
=-cos2α-6sinα=2sin2α-6sinα-1=2(sinα-$\frac{3}{2}$)2-$\frac{11}{2}$,
令t=sinα,根据α∈(0,$\frac{π}{2}$),可得t∈(0,1),则y=2${(t-\frac{3}{2})}^{2}$-$\frac{11}{2}$,
∴当t=0时,y=-1;当t=1时,y=-5,且函数y在(0,1)上单调递减,
∴y∈(-5,-1),
故答案为:(-5,-1).
点评 本题主要考查角的变换及倍角公式在转化函数中的应用,一般来讲考查函数的性质时要转化为基本函数求解,要特别注意α的范围,这是解题的易错点,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.${(\root{3}{x}-\frac{2}{x})^{29}}$展开式中含$\frac{1}{x}$的项是( )
| A. | 第8项 | B. | 第9项 | C. | 第10项 | D. | 第11项 |
6.已知向量$\overrightarrow{α}$,$\overrightarrow{β}$,$\overrightarrow{γ}$ 满足|$\overrightarrow{α}$|=1,$\overrightarrow{α}$⊥($\overrightarrow{α}$-2$\overrightarrow{β}$),($\overrightarrow{α}$-$\overrightarrow{γ}$)⊥($\overrightarrow{β}$-$\overrightarrow{γ}$),若|$\overrightarrow{β}$|=$\frac{\sqrt{17}}{2}$,|$\overrightarrow{γ}$|的最大值和最小值分别为m,n,则m+n等于( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{{\sqrt{15}}}{2}$ |
 ,则
,则 ”的否命题为__________.
”的否命题为__________. 在第一、三象限且不等式组
在第一、三象限且不等式组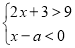 无解的概率是 .
无解的概率是 .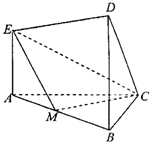 在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.