题目内容
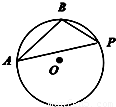
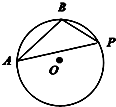如图，半径为1的⊙O上有一定点P和两个动点A，B，且AB=1，则| PA |
| PB |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
分析：可连接OA、OB、OP，设∠AOP=θ，则∠POB=θ+
，将
•
转化为
•
=（
-
）•（
-
）=
•
-
•
-
•
+
2，再利用向量的数量积计算即可．
| π |
| 3 |
| PA |
| PB |
| PA |
| PB |
| OA |
| OP |
| OB |
| OP |
| OA |
| OB |
| OA |
| OP |
| OP |
| OB |
| OP |
解答：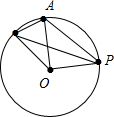
解：连接OA、OB、OP，由|
|=|
|=|
|=1知：∠AOB=
，
设∠AOP=θ，则∠POB=θ+
，于是
•
=（
-
）•（
-
）=
•
-
•
-
•
+
2
=1×1×cos
-1×1×cosθ-1×1×cos（θ+
）+1
=
-[cosθ+cos（θ+
）]
=
-
（
cosθ-
sinθ）
=
-
cos（θ+
）
∴
•
的最大值为：
+
故答案为：
+
解：连接OA、OB、OP，由|| OA |
| OB |
| AB |
| π |
| 3 |
设∠AOP=θ，则∠POB=θ+
| π |
| 3 |
| PA |
| PB |
| OA |
| OP |
| OB |
| OP |
| OA |
| OB |
| OA |
| OP |
| OP |
| OB |
| OP |
=1×1×cos
| π |
| 3 |
| π |
| 3 |
=
| 3 |
| 2 |
| π |
| 3 |
| PA |
=
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| 3 |
| π |
| 6 |
∴
| PA |
| PB |
| 3 |
| 2 |
| 3 |
故答案为：
| 3 |
| 2 |
| 3 |
点评：本题考查余弦函数的定义域和值域，关键在于将
•
进行合理转化，考查转化思想与辅助角公式的运用，属于中档题．
| PA |
| PB |
练习册系列答案
相关题目
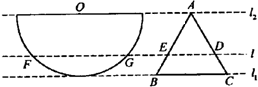（2013•江西）如图，半径为1的半圆O与等边三角形ABC夹在两平行线l1，l2之间，l∥l1，l与半圆相交于F，G两点，与三角形ABC两边相交于E，D两点．设弧
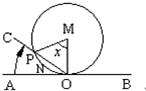如图，半径为1的圆M，切直线AB于点O，射线OC从OA出发，绕O点顺时针方向旋转到OB，旋转过程中OC交⊙M于P，记∠PMO为x，弓形PNO的面积S=f （ x ），那么f （ x ）的图象是
如图，半径为1的圆O上有定点P和两动点A、B，AB=
的最大值是 ．