Question

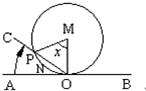如图，半径为1的圆M，切直线AB于点O，射线OC从OA出发，绕O点顺时针方向旋转到OB，旋转过程中OC交⊙M于P，记∠PMO为x，弓形PNO的面积S=f （ x ），那么f （ x ）的图象是
（

A．

B．

C．

D．

Answer 1

分析：写出函数S=f （ x ）的解析式．根据函数的单调性和极值判断出函数图象的大体形状即可．

解答：解：由题意得S=f （ x ）=

1

2

x-

1

2

sinx  f′（x）=

1

2

-

1

2

cosx＞0
当x=0和x=2π时，f′（x）=0，取得极值．
则函数S=f （ x ）在[0，2π]上为增函数，当x=0和x=2π时，取得极值．结合选项，A正确．
故选A．

点评：本题考查了函数的解析式的求法以及函数的求导，根据函数的性质判断函数的图象，求出函数的解析式是解决此题的关键．