题目内容
已知数列{an}的各项均为正数,a1≠2,且前n项之和Sn满足6Sn=a2n+3an+2,求数列的通项公式.
考点:数列递推式,数列的函数特性
专题:点列、递归数列与数学归纳法
分析:在数列递推式中取n=1求得首项,取n=n-1得另一递推式,作差后得到数列{an}是以1为首项,以3为公差的等差数列,然后由等差数列的通项公式得答案.
解答:
解:由6Sn=a2n+3an+2 ①,
当n=1时,有6a1=a12+3a1+2,即a12-3a1+2=0,解得a1=2(舍)或a1=1;
当n>1时,有6Sn-1=an-12+3an-1+2 ②,
①-②得:6an=an2-an-12+3an-3an-1,
即(an+an-1)(an-an-1-3)=0,
∵an>0,
∴an-an-1=3,
则数列{an}是以1为首项,以3为公差的等差数列,
则an=3n-2.
当n=1时,有6a1=a12+3a1+2,即a12-3a1+2=0,解得a1=2(舍)或a1=1;
当n>1时,有6Sn-1=an-12+3an-1+2 ②,
①-②得:6an=an2-an-12+3an-3an-1,
即(an+an-1)(an-an-1-3)=0,
∵an>0,
∴an-an-1=3,
则数列{an}是以1为首项,以3为公差的等差数列,
则an=3n-2.
点评:本题考查了数列递推式,考查了等差关系的确定,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与直线y=b (0<b<A)的三个相邻交点的横坐标分别是2,4,8,则f(x)的单调递增区间是( )
| A、[6kπ,6kπ+3],k∈Z |
| B、[6k-3,6k],k∈Z |
| C、[6k,6k+3],k∈Z |
| D、无法确定 |
sin
•cos(-
)+tan(-
)•tan
的值是( )
| 7π |
| 3 |
| 11π |
| 6 |
| 15π |
| 4 |
| 13π |
| 3 |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、
|
抛物线y=4x2按照向量
=(1,2)平移后,其顶点在一次函数y=
x+
b的图象上,则b的值( )
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
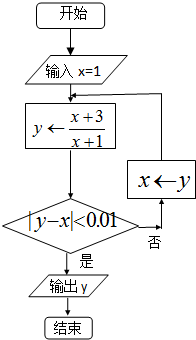 毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数x,x≠
毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数x,x≠