题目内容

设{a_n}为等差数列，S_n为数列{a_n}的前n项和，已知S₇=7，S₁₅=75．
（1）求数列{a_n}的通项公式；
（2）若b_n=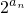 $数学公式$ +3，求数列{b_n}的前n项和T_n．

解：（1）设等差数列{a_n}的公差为d，则 $\text{[math]}$ （1分）
∵S₇=7，S₁₅=75，
∴ $\text{[math]}$ （3分）
即 $\text{[math]}$ 解得a₁=-2，d=2（5分）
∴数列a_n的通项公式为a_n=n-3（6分）
（2） $\text{[math]}$ ，
则T_n=b₁+b₂+b₃++b_n= $\text{[math]}$ = $\text{[math]}$
= $\text{[math]}$ = $\text{[math]}$ （12分）
分析：（1）设出等差数列的首项和公差，然后利用待定系数法根据S₇=7，S₁₅=75求出数列的通项公式即可；
（2）首先根据（1）求出数列{b_n}的通项公式，然后采取分组法求数列{b_n}的前n项和T_n．
点评：本题主要考查等差数列的前n项和的公式以及数列的求和，解题的方法是利用待定系数法，对于等比与等差和的形式的数列，一般采取分组法求前n项和，属于基础题．

练习册系列答案

快乐寒假寒假能力自测系列答案

快乐假期寒假生活系列答案

Happy holiday快乐假期寒假作业延边教育出版社系列答案

快乐练习寒假衔接优计划系列答案

快乐学习寒假作业系列答案

快乐之星学期复习期末加寒假系列答案

鲁人泰斗快乐寒假假期好时光武汉大学出版社系列答案

孟建平寒假练练系列答案

初中综合寒假作业系列答案

本土教辅轻松寒假总复习系列答案

相关题目

设a_n为等差数列，b_n为等比数列，且a₁=0，若c_n=a_n+b_n，且c₁=1，c₂=1，c₃=2．
（1）求a_n的公差d和b_n的公比q；（2）求数列c_n的前10项和．

5、设{a_n}为等差数列，公差d=-2，s_n为其前n项和，若s₁₀=s₁₁，则a₁=（　　）

设{a_n}为等差数列，则下列数列中，成等差数列的个数为（　　）
①{a_n²}　②{pa_n}　③{pa_n+q}　④{na_n}（p、q为非零常数）

设{a_n}为等差数列，S_n为数列{a_n}的前n项和，已知S₇=7，S₁₅=75．
（Ⅰ）求数列{a_n}的通项公式；
（2）令b_n=C an（注释：b_n等于C的a_n次方），（其中C为常数，且C≠0，n∈N^*），求证：数列{b_n}为等比数列．

设{a_n}为等差数列，a₁＞0，a₆+a₇＞0，a₆•a₇＜0则使S_n＞0成立的最大的n为（　　）