题目内容
3.设f(x)是定义在R上的偶函数,且f(2-x)=f(2+x),当x∈[-2,0]时,f(x)=($\frac{\sqrt{2}}{2}$)x-1,记g(x)=f(x)-loga(x+2)(其中a>0,a≠1),试讨论函数g(x)在区间(-2,6]上零点的个数.分析 由f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),推出函数f(x)是以4为最小正周期的函数,结合题意画出在区间(-2,6]上函数f(x)和y=loga(x+2)的图象,注意对a讨论,分a>1,0<a<1,结合图象即可得到结论.
解答 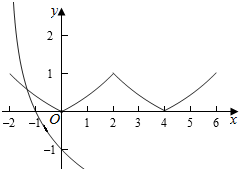 解:∵设f(x)是定义在R上的偶函数,且f(2-x)=f(2+x),
解:∵设f(x)是定义在R上的偶函数,且f(2-x)=f(2+x),
∴且f(2-x)=f(2+x)=f(x-2),
即f(4+x)=f(x),
∴f(x)的周期为4,
若x∈[0,2],则-x∈[-2,0]时,
即f(-x)=($\frac{\sqrt{2}}{2}$)-x-1=f(x),
∴f(x)=($\sqrt{2}$)x-1,x∈[0,2],
由g(x)=f(x)-loga(x+2)=0得f(x)=loga(x+2),
作出函数f(x)在区间[-2,6]上图象如图:
若0<a<1,
∵f(-2)=($\frac{\sqrt{2}}{2}$)-2-1=2-1=1,当x→-2时,g(x)→+∞,
∴此时两个函数有一个交点,即函数g(x)有一个零点,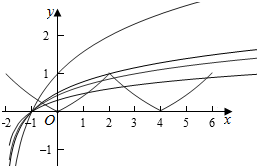
若a>1,∵f(2)=f(6)=1,
设h(x)=loga(x+2),则h(2)=loga4,h(6)=loga8,
当h(2)>1,即loga4>1,得1<a<4时,两个函数有一个交点,此时函数g(x)有一个零点,
当h(2)=1,即loga4=1,得a=4时,两个函数有2个交点,此时函数g(x)有2个零点,
当$\left\{\begin{array}{l}{h(2)<1}\\{h(6)>1}\end{array}\right.$,即$\left\{\begin{array}{l}{lo{g}_{a}4<1}\\{lo{g}_{a}8>1}\end{array}\right.$,即$\left\{\begin{array}{l}{a>4}\\{1<a<8}\end{array}\right.$即4<a<8时,两个函数有3个交点,此时函数g(x)有3个零点,
当h(6)≤1,即loga8≤1,即a≥8时,两个函数有4个交点,此时函数g(x)有4个零点.
点评 本题主要考查函数与方程的应用,以及函数零点个数的判断,利用函数的奇偶性和周期性,作出是f(x)的图象,同时结合数形结合以及分类讨论的数学思想方法,转化为不等式求解是解决本题的关键.综合性较强,有一定的难度.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 充分不必要条件 | B. | 不要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |