题目内容

4．过圆（x-1）2+（y+2）2=16上一点（1，2）的圆的切线方程是y=2．

分析 由题意画出图形，数形结合即可求得过圆（x-1）2+（y+2）2=16上一点（1，2）的圆的切线方程．

解答 解：由圆（x-1）2+（y+2）2=16，得圆心坐标为C（1，-2），
又点P（1，2），
∴过点P且与圆（x-1）2+（y+2）2=16相切得直线平行于x轴，
直线方程为y=2．
故答案为：y=2．

点评 本题考查圆的切线方程，考查数形结合的解题思想方法，是基础题．

练习册系列答案
相关题目
16．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线与直线x-2y+1=0平行，则双曲线的离心率为（　　）
A．$\sqrt{5}$B．$\frac{\sqrt{5}}{2}$C．$\frac{\sqrt{3}}{2}$D．$\sqrt{3}$
16．设双曲线C：$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的左焦点为F（-c，0）（c＞0），P为双曲线C右支上的一点，线段PF与圆x2+y2+$\frac{2c}{3}$x+$\frac{a^2}{9}$=0相切于点Q，且$\overrightarrow{PF}$+3$\overrightarrow{FQ}$=$\overrightarrow 0$，则双曲线C的离心率为$\sqrt{5}$．
12．设平面向量$\overrightarrow a=\overrightarrow{OA}$，定义以x轴非负半轴为始边，逆时针方向为正方向，OA为终边的角称为向量$\overrightarrow a$的幅角．若r1是向量$\overrightarrow a$的模，r2是向量$\overrightarrow b$的模，$\overrightarrow a$的幅角是θ1，$\overrightarrow b$的幅角是θ2，定义$\overrightarrow a?\overrightarrow b$的结果仍是向量，它的模为r1r2，它的幅角为θ1+θ2．给出$\overrightarrow a=（{x_1}，{y_1}），\overrightarrow b=（{x_2}，{y_2}）$．试用$\overrightarrow a$、$\overrightarrow b$的坐标表示$\overrightarrow a?\overrightarrow b$的坐标，结果为$\overrightarrow a?\overrightarrow b=（{x_1}{x_2}-{y_1}{y_2}，{x_1}{y_2}+{x_2}{y_1}）$．
19．在△ABC中，a，b，c分别是内角A，B，C的对边，满足acosB+bcosA=2ccosC．
（Ⅰ）求角C的大小；
（Ⅱ）若△ABC的面积为2$\sqrt{3}$，求边长c的最小值．
9．已知x，y满足约束条件$\left\{\begin{array}{l}{x-2y+4≥0}\\{x+y-2≤0}\\{y≥0}\\{\;}\end{array}\right.$，若目标函数z=ax-y仅在点（0，2）处取得最小值，则a的取值范围是（　　）
A．（-$\frac{1}{2}$，1）B．（-∞，-1）∪（$\frac{1}{2}$，+∞）C．（-1，$\frac{1}{2}$）D．（-∞，-$\frac{1}{2}$）∪（1，+∞）
16．执行如图所示的程序框图，若输出的结果为3，则输入的实数x的值是（　　）
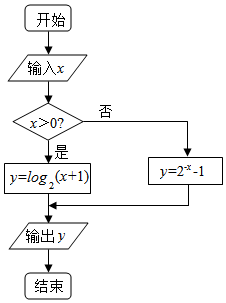
A．-2B．2C．7D．-2或7
13．已知点（-$\sqrt{2}$，0）到双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线的距离为$\frac{\sqrt{5}}{5}$，则该双曲线的离心率为（　　）
A．$\frac{\sqrt{5}}{2}$B．$\sqrt{2}$C．$\frac{\sqrt{10}}{3}$D．$\sqrt{5}$+1
13．已知函数f（x）=sinx，g（x）=$\sqrt{3}$cosx，直线x=m与f（x），g（x）的图象分别交于M，N两点，则|MN|的最大值为（　　）
A．2B．$\sqrt{2}$C．2$\sqrt{2}$D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网