Question

7．①若f（x）是[-4，4]上的单调增函数，且f（2x-1）＜f（x+2），求x的取值范围．
②已知函数f（x）=-x²+|x|，x∈R．将f（x）化成分段函数形式，画出图象并由图象写出f（x）的单调区间．

Answer 1

分析 ①由题意可得，f（2x-1）＜f（x+2），即为-4≤2x-1＜x+2≤4，解不等式即可得到所求范围；
②运用绝对值的含义，可得f（x）的分段函数，再由分段函数的图象画法可得图象，再由图象写出单调区间．

解答 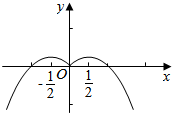解：①由题意可得，f（2x-1）＜f（x+2），即为
$\left\{\begin{array}{l}{-4≤2x-1≤4}\\{-4≤x+2≤4}\\{2x-1＜x+2}\end{array}\right.$，即有$\left\{\begin{array}{l}{-\frac{3}{2}≤x≤\frac{5}{2}}\\{-6≤x≤2}\\{x＜3}\end{array}\right.$，
解得-$\frac{3}{2}$≤x≤2，
则x的取值范围为[-$\frac{3}{2}$，2]；
②f（x）=$\left\{\begin{array}{l}{-{x}^{2}+x，x≥0}\\{-{x}^{2}-x，x＜0}\end{array}\right.$
由分段函数的图象画法，可得f（x）的图象：
由图象可得f（x）的增区间为（-∞，-$\frac{1}{2}$），（0，$\frac{1}{2}$）；
减区间为（-$\frac{1}{2}$，0），（$\frac{1}{2}$，+∞）．

点评 本题考查函数的性质和运用，考查单调性的运用和不等式的解法，同时考查分段函数的图象和运用：求单调区间，属于中档题．