题目内容
已知函数 ,y=f(x)的部分图象如图,则
,y=f(x)的部分图象如图,则 =
=
- A.

- B.

- C.

- D.

B
分析:根据函数的图象,求出函数的周期,然后求出ω,确定A的值,根据(0.1)确定φ的值,求出函数的解析式,然后求出 即可.
即可.
解答:由题意可知A=1,T= ,所以ω=2,函数的解析式为:f(x)=Atan(ωx+φ)(因为函数过(0,1),所以,1=tanφ,所以φ=
,所以ω=2,函数的解析式为:f(x)=Atan(ωx+φ)(因为函数过(0,1),所以,1=tanφ,所以φ= ,
,
所以f(x)=tan(2x+ )则f(
)则f(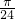 )=tan(
)=tan(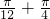 )=
)=
故选B
点评:本题是基础题,考查正切函数的图象的求法,确定函数的解析式的方法,求出函数值,考查计算能力.
分析:根据函数的图象,求出函数的周期,然后求出ω,确定A的值,根据(0.1)确定φ的值,求出函数的解析式,然后求出
 即可.
即可.解答:由题意可知A=1,T=
 ,所以ω=2,函数的解析式为:f(x)=Atan(ωx+φ)(因为函数过(0,1),所以,1=tanφ,所以φ=
,所以ω=2,函数的解析式为:f(x)=Atan(ωx+φ)(因为函数过(0,1),所以,1=tanφ,所以φ= ,
,所以f(x)=tan(2x+
 )则f(
)则f(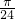 )=tan(
)=tan(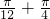 )=
)=
故选B
点评:本题是基础题,考查正切函数的图象的求法,确定函数的解析式的方法,求出函数值,考查计算能力.

练习册系列答案
相关题目
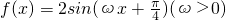 ,y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,
,y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,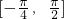 上的最大值和最小值.
上的最大值和最小值.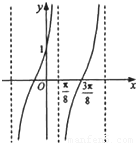 已知函数
已知函数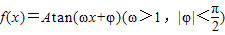 ,y=f(x)的部分图象如图,则
,y=f(x)的部分图象如图,则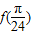 =( )
=( )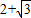
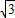
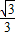
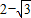
 ,试求函数y=f(x)的解析式;
,试求函数y=f(x)的解析式; .时,求a的取值范围.
.时,求a的取值范围.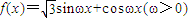 ,y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则ω= .
,y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则ω= .