题目内容
已知函数,y=f(x)=-x3+ax2+b(a,b∈R)(I )要使f(x)在(0,1)上单调递增,求a的取值范围;
(II)当a>0时,若函数f(x)的极小值和极大值分别为1、
 ,试求函数y=f(x)的解析式;
,试求函数y=f(x)的解析式;III 若x∈[0,1]时,y=f(x)图象上任意一点处的切线倾斜角为θ,当≤θ≤
 .时,求a的取值范围.
.时,求a的取值范围.
【答案】分析:(I)先求导函数f′(x),要使f(x)在区间(0,1)上单调递增,只需x∈(0,1)时,f′(x)>0恒成立,然后转化成 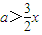 恒成立,即可求出a的范围;
恒成立,即可求出a的范围;
(II)由(I)中导函数的解析式,我们易求出函数取极值时x的值,然后根据函数f(x)的极小值和极大值分别为1、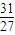 ,构造关于a,b的方程,解方程后即可求出函数y=f(x)的解析式;
,构造关于a,b的方程,解方程后即可求出函数y=f(x)的解析式;
(III)根据导数的几何意义可知tanθ=f′(x),然后根据倾斜角为θ的范围求出f′(x)的范围在x∈[0,1]恒成立,将a分离出来,使之恒成立即可求出a的范围.
解答:解:(I)f′(x)=-3x2+2ax,
由题设,当x∈(0,1)时,f′(a)>0恒成立,
即-3x2+2ax>0恒成立,
∴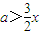 恒成立,
恒成立,
∴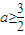
(II)由(I)得,令f′(x)=-3x2+2ax=0
则x=0,或x=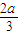
又∵a>0时,函数f(x)的极小值和极大值分别为1、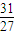 ,
,
故f(0)=1,f(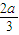 )=
)=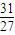
解得a=1,b=1
∴f(x)=-x3+x2+1
(III)当x∈[0,1]时,tanθ=f′(x)=-3xh3+2ax
∵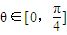 .∴0≤f'(x)≤1.
.∴0≤f'(x)≤1.
∴0≤-3x2+2ax≤1
在x∈[0,1]恒成立,由(1)知,当-3x2+2ax≥0时,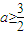 ,
,
由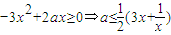 恒成立,
恒成立,
又 ,∴
,∴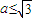
∴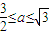
点评:本小题主要考查函数的概念、性质、图象及导数等基础知识,考查灵活运用转化与划归的思想方法进行探索、分析与解决问题的综合能力,属于中档题.
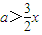 恒成立,即可求出a的范围;
恒成立,即可求出a的范围;(II)由(I)中导函数的解析式,我们易求出函数取极值时x的值,然后根据函数f(x)的极小值和极大值分别为1、
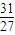 ,构造关于a,b的方程,解方程后即可求出函数y=f(x)的解析式;
,构造关于a,b的方程,解方程后即可求出函数y=f(x)的解析式;(III)根据导数的几何意义可知tanθ=f′(x),然后根据倾斜角为θ的范围求出f′(x)的范围在x∈[0,1]恒成立,将a分离出来,使之恒成立即可求出a的范围.
解答:解:(I)f′(x)=-3x2+2ax,
由题设,当x∈(0,1)时,f′(a)>0恒成立,
即-3x2+2ax>0恒成立,
∴
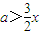 恒成立,
恒成立,∴
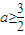
(II)由(I)得,令f′(x)=-3x2+2ax=0
则x=0,或x=
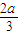
又∵a>0时,函数f(x)的极小值和极大值分别为1、
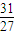 ,
,故f(0)=1,f(
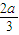 )=
)=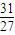
解得a=1,b=1
∴f(x)=-x3+x2+1
(III)当x∈[0,1]时,tanθ=f′(x)=-3xh3+2ax
∵
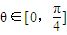 .∴0≤f'(x)≤1.
.∴0≤f'(x)≤1.∴0≤-3x2+2ax≤1
在x∈[0,1]恒成立,由(1)知,当-3x2+2ax≥0时,
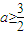 ,
,由
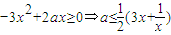 恒成立,
恒成立,又
 ,∴
,∴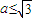
∴
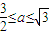
点评:本小题主要考查函数的概念、性质、图象及导数等基础知识,考查灵活运用转化与划归的思想方法进行探索、分析与解决问题的综合能力,属于中档题.

练习册系列答案
相关题目
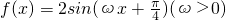 ,y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,
,y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,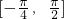 上的最大值和最小值.
上的最大值和最小值.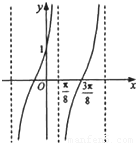 已知函数
已知函数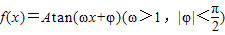 ,y=f(x)的部分图象如图,则
,y=f(x)的部分图象如图,则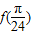 =( )
=( )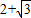
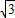
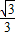
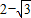
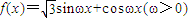 ,y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则ω= .
,y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则ω= .