题目内容
(本题满分14分)已知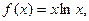
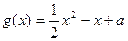 .
.
(1)当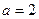 时,求
时,求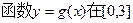 上的值域;
上的值域;
(2) 求函数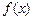 在
在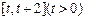 上的最小值;
上的最小值;
(3) 证明: 对一切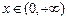 ,都有
,都有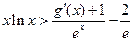 成立
成立
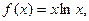
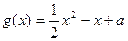 .
.(1)当
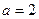 时,求
时,求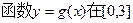 上的值域;
上的值域;(2) 求函数
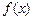 在
在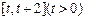 上的最小值;
上的最小值;(3) 证明: 对一切
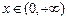 ,都有
,都有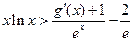 成立
成立解(1)∵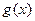 =
=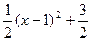 , x∈[0,3] ………….. 1分
, x∈[0,3] ………….. 1分
当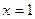 时,
时,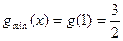 ;当
;当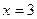 时,
时,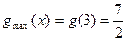
故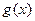 值域为
值域为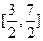 ………………. 3分
………………. 3分
(2)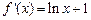 ,当
,当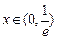 ,
,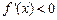 ,
,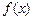 单调递减,当
单调递减,当 ,
,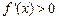 ,
,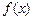 单调递增. …………………………. 5分
单调递增. …………………………. 5分
①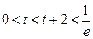 ,t无解; …………… 6分
,t无解; …………… 6分
②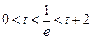 ,即
,即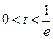 时,
时,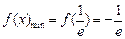 ; ………………. 7分
; ………………. 7分
③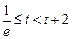 ,即
,即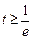 时,
时,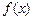 在
在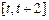 上单调递增,
上单调递增,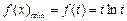 ;……8分
;……8分
所以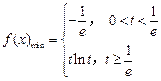 . ………………. 9分
. ………………. 9分
(3)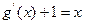 ,所以问题等价于证明
,所以问题等价于证明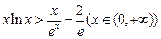 ,由(2)可知
,由(2)可知
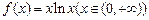 的最小值是
的最小值是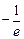 ,当且仅当
,当且仅当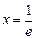 时取到;………….. 11分
时取到;………….. 11分
设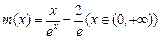 ,则
,则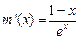 ,易得
,易得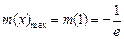 ,当且仅当
,当且仅当 时
时
取到,从而对一切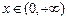 ,都有
,都有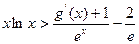 成立. …………….. 14分
成立. …………….. 14分
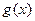 =
=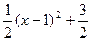 , x∈[0,3] ………….. 1分
, x∈[0,3] ………….. 1分当
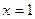 时,
时,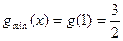 ;当
;当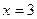 时,
时,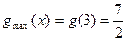
故
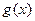 值域为
值域为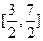 ………………. 3分
………………. 3分(2)
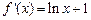 ,当
,当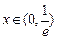 ,
,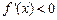 ,
,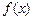 单调递减,当
单调递减,当 ,
,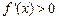 ,
,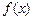 单调递增. …………………………. 5分
单调递增. …………………………. 5分①
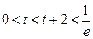 ,t无解; …………… 6分
,t无解; …………… 6分②
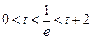 ,即
,即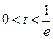 时,
时,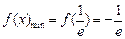 ; ………………. 7分
; ………………. 7分③
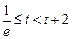 ,即
,即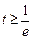 时,
时,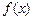 在
在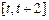 上单调递增,
上单调递增,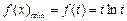 ;……8分
;……8分所以
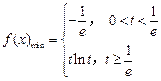 . ………………. 9分
. ………………. 9分(3)
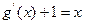 ,所以问题等价于证明
,所以问题等价于证明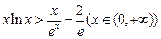 ,由(2)可知
,由(2)可知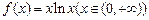 的最小值是
的最小值是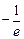 ,当且仅当
,当且仅当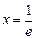 时取到;………….. 11分
时取到;………….. 11分 设
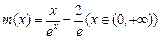 ,则
,则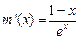 ,易得
,易得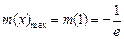 ,当且仅当
,当且仅当 时
时取到,从而对一切
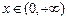 ,都有
,都有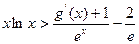 成立. …………….. 14分
成立. …………….. 14分略

练习册系列答案
相关题目
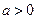 ,函数
,函数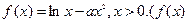 的图像连续不断)
的图像连续不断)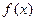 的单调区间;
的单调区间;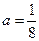 时,证明:存在
时,证明:存在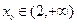 ,使
,使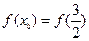 ;
;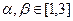 ,且
,且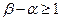 ,使
,使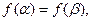 证明
证明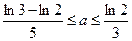 .
.
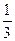 ,2]都有|f(x)|≤1
,2]都有|f(x)|≤1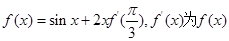 的导函数,令
的导函数,令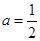 ,
,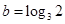 ,则下列关系正确的是( )
,则下列关系正确的是( )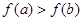
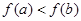
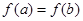
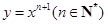 在点(1,1)处的切线与
在点(1,1)处的切线与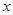 轴的交点的横坐标为
轴的交点的横坐标为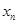 ,则
,则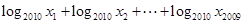 的值为( )
的值为( )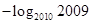
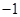
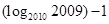
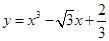 上的任意一点,p点处切线倾斜角为a,则角a的取值范围是( )
上的任意一点,p点处切线倾斜角为a,则角a的取值范围是( )




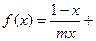 1n
1n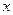 ,且
,且 >0
>0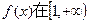 上是增函数,求
上是增函数,求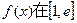 的最大值和最小值。
的最大值和最小值。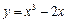 在点(1,-1)处的切线方程是 .
在点(1,-1)处的切线方程是 .