题目内容
 下列命题:
下列命题:(1)若函数f(x)=lg(x+
| x2+a |
(2)函数f(x)=|sin2x|的周期T=
| π |
| 2 |
(3)方程log6x=cosx有且只有三个实数根;
(4)对于函数f(x)=x2,若0<x1<x2,则f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
以上命题为真命题的是
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:判断a=1时,函数f(x)=lg(x+
)的奇偶性,可判断(1);求出函数f(x)=|sin2x|的周期,可判断(2);数形结合,分析方程log6x=cosx根的个数,可判断③;判断函数f(x)=x2的凸凹性,可判断(4)
| x2+a |
解答:
解:(1)当a=1时,f(x)=lg(x+
)的定义域R关于原点对称,
且f(-x)+f(x)=lg(-x+
)+lg(x+
)=lg[(
)2-x2]=lg1=0,
故此时函数f(x)=lg(x+
)为奇函数,故(1)错误;
函数y=sin2x的周期T=π,纵向对折变换后函数f(x)=|sin2x|的周期T=
,故(2)正确;
作出y=log6x与y=cosx的图象,如下图所示:
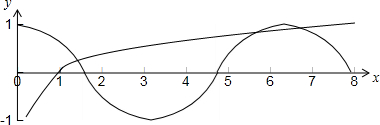
由两个函数图象有且只有三个交点,可得方程log6x=cosx有且只有三个实数根,故(3)正确;
∵函数f(x)=x2是凹函数,∴在0<x1<x2,则0<x1<x2,则f(
)<
,故(4)正确;
故真命题是:(2)(3)(4),
故答案为:(2)(3)(4)
| x2+1 |
且f(-x)+f(x)=lg(-x+
| x2+1 |
| x2+1 |
| x2+1 |
故此时函数f(x)=lg(x+
| x2+a |
函数y=sin2x的周期T=π,纵向对折变换后函数f(x)=|sin2x|的周期T=
| π |
| 2 |
作出y=log6x与y=cosx的图象,如下图所示:

由两个函数图象有且只有三个交点,可得方程log6x=cosx有且只有三个实数根,故(3)正确;
∵函数f(x)=x2是凹函数,∴在0<x1<x2,则0<x1<x2,则f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故真命题是:(2)(3)(4),
故答案为:(2)(3)(4)
点评:本题考查的知识点是命题的真假判定,同时考查了函数的一些性质,注意数形结合的方法.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
甲、乙2人下棋,下成和棋的概率是
,乙获胜的概率是
,则甲不胜的概率是( )
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
sin
•cos(-
)+tan(-
)•tan
的值是( )
| 7π |
| 3 |
| 11π |
| 6 |
| 15π |
| 4 |
| 13π |
| 3 |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、
|
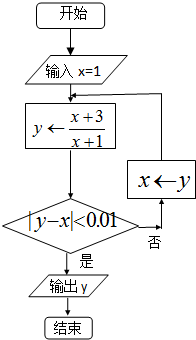 毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数x,x≠
毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数x,x≠