题目内容
已知椭圆
的左焦点
,
为坐标原点,点
在椭圆上,点
在椭圆的右准线上,若
,则椭圆的离心率为 ．
的左焦点,为坐标原点,点在椭圆上,点在椭圆的右准线上,若,则椭圆的离心率为 ．
试题分析：因为
，所以
,又因为
表示与
同向的单位向量，所以
在
的平分线上，所以四边形
为菱形，所以
,设点
，因为点在椭圆的右准线上,则点
，因为，所以
，由因为，所以
，代入坐标进行运算，结合
，可以计算出椭圆的离心率为.点评：解决本题的关键在于发现四边形
为菱形，所以对角线互相垂直，从而转化成向量的数量积为0进行求解，本题运算量比较大，求解时要仔细.
练习册系列答案
科学实验活动册系列答案
相关题目
．
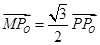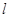：y=kx+m(m≠0)与（Ⅰ）中的轨迹C交于不同的两点A，B．
的左、右两焦点分别为
，点
在椭圆上，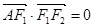
，
，则椭圆的离心率
等于 ( )
有相同的焦点，直线y=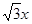
为
的一条渐近线. 
(0,4)的直线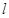
，交双曲线
点（
=
，且
时，求
与曲线
相切于点
，则
的值为 ( )
的焦点为
，准线为
，过
；
的值．
(a>0,b>0)的两个焦点，A和B是以O为圆心，以｜OF1｜为半径的圆与该左半椭圆的两个交点，且△F2AB是等边三角形，则椭圆的离心率为( )
-1
的焦点在
轴上,长轴长是短轴长的两倍,则m的值为 ( )
