题目内容
(本题满分12分)一座拱桥桥洞的截面边界由抛物线弧段 和矩形
和矩形 的三边组成,拱的顶部
的三边组成,拱的顶部 距离水面
距离水面 ,水面上的矩形的高度为
,水面上的矩形的高度为 ,水面宽
,水面宽 ,如图所示.一艘船运载一个长方体形的集装箱,此箱平放在船上.已知船宽
,如图所示.一艘船运载一个长方体形的集装箱,此箱平放在船上.已知船宽 ,船面距离水面
,船面距离水面 ,集装箱的尺寸为长×宽×高=
,集装箱的尺寸为长×宽×高= .试问此船能否通过此桥?并说明理由.
.试问此船能否通过此桥?并说明理由.

不能通过此桥.
【解析】
试题分析:解函数应用问题的步骤1.审题:弄清题意,分清条件和结论,理顺数量关系,初步选择数学模型;2.建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型;3.解模:求解数学模型,得出数学结论;本题建立适当的直角坐标系即可完成.
试题解析:
建立如图所示的平面直角坐标系,使抛物线顶点O在坐标原点,对称轴与y轴重合,设抛物线方程为
 2分
2分

由题设条件知 在抛物线上,
在抛物线上,
∴ ,
, 即抛物线方程为
即抛物线方程为 6分
6分
集装箱最高处 关于
关于 轴对称.
轴对称.
于是设 ,则
,则 .
.
∴ 此时点
此时点 距离水面的高度为5-0.75=4.25 10分
距离水面的高度为5-0.75=4.25 10分
而集装箱高加船高为3+1.5=4.5>4.25,故此船不能通过此桥 . 12分
考点:抛物线及其应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 “
“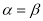 ”是“
”是“ ”的
”的 =( )
=( )  B.
B. C.
C. D.
D.
 的解,下列判断不正确的是 ( )
的解,下列判断不正确的是 ( ) 时,无解 B.
时,无解 B. 时,2个解
时,2个解 
 时,4个解 D.
时,4个解 D.
 时,无解
时,无解 ,则
,则
 ( )
( ) B.
B. C.
C. D.
D.
 分别为
分别为 和椭圆
和椭圆 上的点,则
上的点,则 分别是双曲线
分别是双曲线 的左右焦点,过
的左右焦点,过 做垂直于
做垂直于 轴的直线交双曲线于
轴的直线交双曲线于 两点,若
两点,若 为钝角三角形,则双曲线的离心率的范围是
为钝角三角形,则双曲线的离心率的范围是 B.
B.
 D.
D.
 ,
, ,点
,点 在
在 轴上,且点
轴上,且点 的距离相等,则点
的距离相等,则点