题目内容
焦点在x轴上的双曲线,它的两条渐近线的夹角为
,焦距为6,求此双曲线方程为 .
| π |
| 3 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设双曲线方程为
-
=1(a>0,b>0),利用两条渐近线的夹角为
,焦距为6,可得
=
,a2+b2=9,求出a,b,即可求出双曲线方程.
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
| b |
| a |
| ||
| 3 |
解答:
解:设双曲线方程为
-
=1(a>0,b>0),
∵两条渐近线的夹角为
,焦距为6,
∴
=
,a2+b2=9,
∴b=
,a=
,
∴双曲线方程为
-
=1,
故答案为:
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵两条渐近线的夹角为
| π |
| 3 |
∴
| b |
| a |
| ||
| 3 |
∴b=
| 3 |
| 2 |
3
| ||
| 2 |
∴双曲线方程为
| x2 | ||
|
| y2 | ||
|
故答案为:
| x2 | ||
|
| y2 | ||
|
点评:本题考查双曲线方程的求法,是基础题,解题时要认真审题,注意双曲线性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=esinx(-π≤x≤π)的大致图象为( )
A、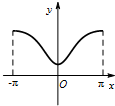 |
B、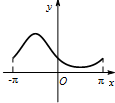 |
C、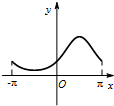 |
D、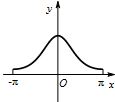 |
 程序框图如图,若输出的s值为两位数时,则n的值为( )
程序框图如图,若输出的s值为两位数时,则n的值为( )| A、3 | B、4 | C、5 | D、6 |
有50件产品,编号1-50,现在从中抽取5件检验,用系统抽样方法确定所抽的编号为( )
| A、5,10,15,20,25 |
| B、5,8,31,36,41 |
| C、5,15,25,35,45 |
| D、2,14,26,38,50 |
已知A(1,
),B(
-2,1),且
•
=0,sinβ≠0,sinα-kcosβ=0,则k=( )
| sinα |
| sin(α+2β) |
| sinα |
| sin(α-2β) |
| OA |
| OB |
A、
| ||||
B、-
| ||||
C、
| ||||
| D、以上都不对 |