题目内容
计算sin47°cos17°-cos47°cos73°的结果为
- A.
- B.
- C.
- D.
A
分析：利用诱导公式把要求的式子化为 sin47°cos17°-cos47°sin17°，再利用两角差的正弦公式化为sin30°，从而求得结果．
解答：sin47°cos17°-cos47°cos73°=sin47°cos17°-cos47°sin17°
=sin（47°-17°）=sin30°=，
故选A．
点评：本题主要考查诱导公式、两角差的正弦公式的应用，特殊角的三角函数的值，属于基础题．
分析：利用诱导公式把要求的式子化为 sin47°cos17°-cos47°sin17°，再利用两角差的正弦公式化为sin30°，从而求得结果．
解答：sin47°cos17°-cos47°cos73°=sin47°cos17°-cos47°sin17°
=sin（47°-17°）=sin30°=
，故选A．
点评：本题主要考查诱导公式、两角差的正弦公式的应用，特殊角的三角函数的值，属于基础题．
练习册系列答案
相关题目
（2）
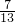，则x2sinθ-y2cosθ=1表示
表示椭圆”的充要条件．其中真命题的个数是________个．