题目内容
为了得到函数f（x）=cos（
+
）的图象，只需将函数f（x）=cos
的图象（ ）
| x |
| 3 |
| π |
| 6 |
| x |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：根据函数y=Asin（ωx+φ）的图象变换直接由自变量x的变化得到答案．
解答：
解：函数y=cos（
+
）=cos[
（x+
）]是把函数y=cosx的自变量由x变为x+
，
根据函数图象平移的法则可知，为了得到函数y=cos（
+
）的图象，
只需把函数y=cos
图象向左平移
个单位即可．
故选：A．
| x |
| 3 |
| π |
| 6 |
| 1 |
| 3 |
| π |
| 2 |
| π |
| 2 |
根据函数图象平移的法则可知，为了得到函数y=cos（
| x |
| 3 |
| π |
| 6 |
只需把函数y=cos
| x |
| 3 |
| π |
| 2 |
故选：A．
点评：本题主要考查函数y=Asin（ωx+φ）的图象变换，三角函数的平移原则为左加右减上加下减，属于基础题．
练习册系列答案
相关题目
已知直线l1：（1-a）x+ay-2=0，l2：ax+（2a+1）y+3=0，则“a=-2”是“l1⊥l2”成立的（ ）
| A、充分不变要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
若a＞b＞0，c＜d＜0，则一定有（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
执行如图所示的程序框图，输出的S值为（ ）
| A、7 | B、8 | C、16 | D、24 |
当a＞l时，函数f （x）=logax和g（x）=（l-a）x的图象的交点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
一个四棱锥的三视图如图所示，则该四棱锥的侧面中，直角三角形的个数为（ ）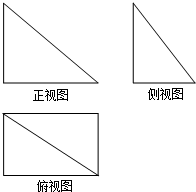
| A、1 | B、2 | C、3 | D、4 |
下列函数是奇函数的是（ ）
| A、f（x）=cosx | ||
| B、f（x）=x3+1 | ||
C、f（x）=x+
| ||
| D、f（x）=log2x |