题目内容
为考察某种甲型H1N1疫苗的效果,进行动物实验,得到如下疫苗效果的实验列联表:
| 感染 | 未感染 | 总计 | |
| 没服用 | 20 | 30 | 50 |
| 服用 | x | y | 50 |
| 总计 | M | N | 100 |
 P(η=2)
P(η=2)(1)求出列联表中数据x,y,M,N的值;
(2)写出ξ与η的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
(3)能够以97.5%的把握认为这种甲型H1N1疫苗有效么?并说明理由.
参考数据:
| P(K2≥k0) | 0.05 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
解:(1)∵P(ξ=2)= P(η=2)
P(η=2)
P(ξ=2)= ,P(η=2)=
,P(η=2)=
∴

∴x=10,x=-9(舍去)
于是y=50-x=40,M=20+x=30,N=30+y=70.
(2)Eξ= ,Eη=
,Eη= ,
,
有Eξ>Eη,说明服用疫苗的两只动物感染数的平均值大于不服用疫苗的两只动物的感染数的平均值,实际意义即表明这种甲型疫苗有效.
(3) =
=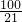 =4.762
=4.762
∵50.24>4.762
∴不能够以97.5%的把握认为这种甲型H1N1疫苗有效
分析:(1)根据所给的两个变量概率之间的关系,写出两个变量对应的概率,得到关于x的方程,解方程即可,做出要求的值.
(2)做出两个变量的期望值,得到服用疫苗的两只动物感染数的平均值大于不服用疫苗的两只动物的感染数的平均值,实际意义即表明这种甲型疫苗有效.
(3)根据所给的数据做出观测值,把观测值同临界值进行比较得到不能够以97.5%的把握认为这种甲型H1N1疫苗有效
点评:本题考查独立性检验的应用,本题解题的关键是正确运算出要用的观测值,把观测值同临界值进行比较,理解概率的意义.
 P(η=2)
P(η=2)P(ξ=2)=
 ,P(η=2)=
,P(η=2)=
∴


∴x=10,x=-9(舍去)
于是y=50-x=40,M=20+x=30,N=30+y=70.
(2)Eξ=
 ,Eη=
,Eη= ,
,有Eξ>Eη,说明服用疫苗的两只动物感染数的平均值大于不服用疫苗的两只动物的感染数的平均值,实际意义即表明这种甲型疫苗有效.
(3)
 =
=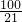 =4.762
=4.762∵50.24>4.762
∴不能够以97.5%的把握认为这种甲型H1N1疫苗有效
分析:(1)根据所给的两个变量概率之间的关系,写出两个变量对应的概率,得到关于x的方程,解方程即可,做出要求的值.
(2)做出两个变量的期望值,得到服用疫苗的两只动物感染数的平均值大于不服用疫苗的两只动物的感染数的平均值,实际意义即表明这种甲型疫苗有效.
(3)根据所给的数据做出观测值,把观测值同临界值进行比较得到不能够以97.5%的把握认为这种甲型H1N1疫苗有效
点评:本题考查独立性检验的应用,本题解题的关键是正确运算出要用的观测值,把观测值同临界值进行比较,理解概率的意义.

练习册系列答案
相关题目


 ,若向量
,若向量 的夹角与
的夹角与 的夹角相等,则实数λ的值为________.
的夹角相等,则实数λ的值为________. =(2,-1,3),
=(2,-1,3), =(-4,2,x),且
=(-4,2,x),且 ,则实数x的值为
,则实数x的值为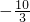

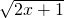 =x+a有两个不同的实数解时,实数a的满足的条件.
=x+a有两个不同的实数解时,实数a的满足的条件. (a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为30°的直线交双曲线右支于M点,若MF2垂直于x轴,则双曲线的离心率为
(a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为30°的直线交双曲线右支于M点,若MF2垂直于x轴,则双曲线的离心率为



