题目内容
利用函数图象判定方程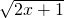 =x+a有两个不同的实数解时,实数a的满足的条件.
=x+a有两个不同的实数解时,实数a的满足的条件.
解:我们在同一平面直角坐标系中分别画出
函数y=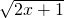 和y=x+a的图象,如下图所示:
和y=x+a的图象,如下图所示:

∵y'=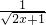 ,故当y=x+a与函数y=
,故当y=x+a与函数y=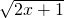 的图象相切时,x=1
的图象相切时,x=1
即此时a=1,结合上图我们易得:方程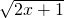 =x+a有两个不同的实数解时
=x+a有两个不同的实数解时
实数a的满足的条件为: ≤a<1
≤a<1
分析:在同一坐标系中画出两个函数y=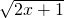 和y=x+a的图象,分析图象关系后,我们易得,满足条件的a能使直线y=x+a夹在函数y=
和y=x+a的图象,分析图象关系后,我们易得,满足条件的a能使直线y=x+a夹在函数y=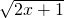 的图象的切线与过端点(-
的图象的切线与过端点(- ,0)的直线之间,利用导数求出切线对应的a值后,即可得到实数a的满足的条件.
,0)的直线之间,利用导数求出切线对应的a值后,即可得到实数a的满足的条件.
点评:本题考查的知识点是根的存在性及根的个数判断,其中利用图象分析实数a的满足的条件,是解答本题的关键.
函数y=
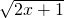 和y=x+a的图象,如下图所示:
和y=x+a的图象,如下图所示:
∵y'=
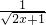 ,故当y=x+a与函数y=
,故当y=x+a与函数y=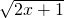 的图象相切时,x=1
的图象相切时,x=1即此时a=1,结合上图我们易得:方程
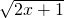 =x+a有两个不同的实数解时
=x+a有两个不同的实数解时实数a的满足的条件为:
 ≤a<1
≤a<1分析:在同一坐标系中画出两个函数y=
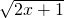 和y=x+a的图象,分析图象关系后,我们易得,满足条件的a能使直线y=x+a夹在函数y=
和y=x+a的图象,分析图象关系后,我们易得,满足条件的a能使直线y=x+a夹在函数y=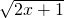 的图象的切线与过端点(-
的图象的切线与过端点(- ,0)的直线之间,利用导数求出切线对应的a值后,即可得到实数a的满足的条件.
,0)的直线之间,利用导数求出切线对应的a值后,即可得到实数a的满足的条件.点评:本题考查的知识点是根的存在性及根的个数判断,其中利用图象分析实数a的满足的条件,是解答本题的关键.

练习册系列答案
相关题目
 =x+a有两个不同的实数解时,实数a的满足的条件.
=x+a有两个不同的实数解时,实数a的满足的条件.