题目内容
(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标系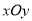 中,直线
中,直线 的方程为
的方程为 ,曲线
,曲线 的参数方程
的参数方程 (
( 为参数)
为参数)
(I)已知在极坐标系(与直角坐标系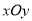 取相同的长度单位,且以原点
取相同的长度单位,且以原点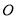 为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点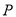 的极坐标
的极坐标 ,判断点
,判断点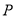 与直线
与直线 的位置关系;
的位置关系;
(II)设点 为曲线
为曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
(I)见解析;(II)
【解析】
试题分析:(I)把极坐标系下的点 化为直角坐标,得P(0,4)容易验证点P在直线
化为直角坐标,得P(0,4)容易验证点P在直线 上;(II)设点Q的坐标为
上;(II)设点Q的坐标为 点Q到直线
点Q到直线 的距离为
的距离为
 即可求得最小值
即可求得最小值
试题解析:(I)把极坐标系下的点 化为直角坐标,得P(0,4)。 1分
化为直角坐标,得P(0,4)。 1分
因为点P的直角坐标(0,4)满足直线 的方程
的方程 ,
,
所以点P在直线 上. 3分
上. 3分
(II)因为点Q在曲线C上,故可设点Q的坐标为 , 4分
, 4分
从而点Q到直线 的距离为
的距离为
 , 6分
, 6分
由此得,当 时,d取得最小值
时,d取得最小值 7分
7分
考点:参数方程

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =
= B.
B. C.
C. D.
D.
 ,
, ,
, .如果
.如果 ,对
,对 都有
都有 ,则
,则 等于
等于  B.
B. C.
C. D.
D.
 :“
:“ ”是“
”是“ ”的充要条件,命题
”的充要条件,命题 :“
:“ ”的否定是“
”的否定是“ ”
” ”为真 B.“
”为真 B.“ ”为真 C.
”为真 C. 真
真 假 D.
假 D. 均为假
均为假  是正方形,
是正方形,  平面
平面 ,
,  .
.
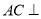
 ;
; 的椭圆,
的椭圆, 为顶点,过右焦点的弦
为顶点,过右焦点的弦 的长度为
的长度为 ,中心
,中心 到弦
到弦 的距离为
的距离为 ,点
,点 从右顶点
从右顶点 开始按逆时针方向在椭圆上移动到
开始按逆时针方向在椭圆上移动到 停止,当
停止,当 时,记
时,记 ,当
,当 ,记
,记 ,函数
,函数 图像是 ( )
图像是 ( ) 




 的内角
的内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,
, ,
, .
. ;
; ,求
,求 .
.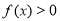 ;
;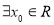 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.