题目内容
如图, 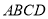 是正方形,
是正方形, 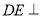 平面
平面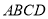 ,
, ,
, 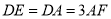 .
.

(Ⅰ) 求证: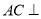
 ;
;
(Ⅱ) 求面FBE和面DBE所形成的锐二面角的余弦值.
(I)见解析;(II)
【解析】
试题分析:(Ⅰ)在证明线线垂直,一般通过证明线面垂直得到,本题中因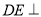 平面
平面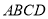 ,
,
所以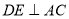 . 因
. 因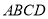 是正方形,所以
是正方形,所以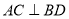 ,所以
,所以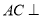 平面
平面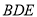 ,从而
,从而 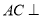
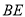 ;(Ⅱ)因
;(Ⅱ)因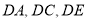 两两垂直,所以可通过建立空间直角坐标系来求解,设
两两垂直,所以可通过建立空间直角坐标系来求解,设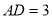 ,可知
,可知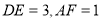 则
则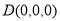 ,
,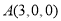 ,
,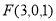 ,
,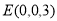 ,
,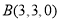 ,
,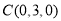 ,通过计算可求得平面
,通过计算可求得平面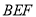 的法向量为
的法向量为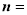
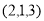
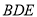 的法向量
的法向量 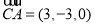 所以
所以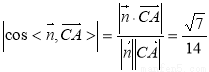
试题解析:(Ⅰ)证明: 因为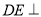 平面
平面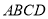 ,
,
所以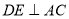 . 1分
. 1分
因为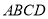 是正方形,
是正方形,
所以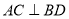 ,
,
所以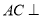 平面
平面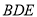 , 3分
, 3分
从而 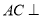
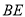 4分
4分
(Ⅱ)【解析】
因为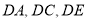 两两垂直,
两两垂直,
所以建立空间直角坐标系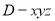 如图所示. 5分
如图所示. 5分
设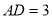 ,可知
,可知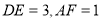 . 6分
. 6分
则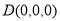 ,
,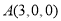 ,
,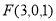 ,
,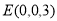 ,
,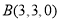 ,
,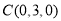 ,
,
所以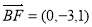 ,
,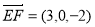 , 7分
, 7分
设平面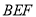 的法向量为
的法向量为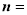
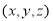 ,则
,则 ,即
,即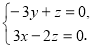 ,
,
令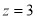 ,则
,则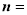
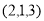 . 10分
. 10分
因为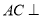 平面
平面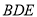 ,所以
,所以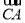 为平面
为平面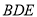 的法向量,
的法向量, 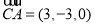 ,
,
所以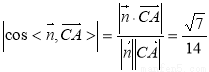 12分
12分
所以面FBE和面DBE所形成的锐二面角的余弦值为 . 13分
. 13分
考点:立体几何

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
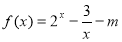 的一个零点在区间(1,3)内,则实数
的一个零点在区间(1,3)内,则实数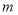 的取值范围是
的取值范围是 的共轭复数是
的共轭复数是 B.
B.  C.
C.  D.
D. 
 内有零点且单调递增的是
内有零点且单调递增的是  B.
B. C.
C. D.
D.
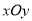 中,直线
中,直线 的方程为
的方程为 ,曲线
,曲线 的参数方程
的参数方程 (
( 为参数)
为参数)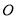 为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点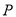 的极坐标
的极坐标 ,判断点
,判断点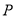 与直线
与直线 为曲线
为曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 中,三个角
中,三个角 的对边边长分别为
的对边边长分别为 ,则
,则 的值为 .
的值为 . ,
, ,
, ,则下列结论正确的是 ( )
,则下列结论正确的是 ( ) B.
B. C.
C. D.
D.
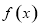 是定义在
是定义在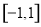 上的奇函数,对于任意
上的奇函数,对于任意 ,
,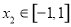 ,
, 总有
总有 且
且 .若对于任意
.若对于任意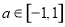 ,存在
,存在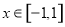 ,使
,使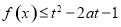 成立,则实数
成立,则实数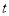 的取值范围是( )
的取值范围是( )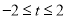 B.
B. 或
或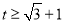
 或
或 D.
D.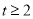 或
或 或
或
 中,底面
中,底面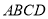 是菱形,
是菱形,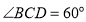 ,四边形
,四边形 是正方形,且
是正方形,且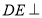 平面
平面
 平面
平面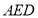 ;
; ,求多面体
,求多面体 的体积
的体积 .
.