题目内容
(本题满分10分)选修4-5: 不等式选讲
设函数 .
.
(Ⅰ)解不等式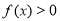 ;
;
(Ⅱ)若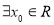 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
(1) ,(2)
,(2) ,
,
【解析】
试题分析:首先利用零点分区间讨论去掉绝对值符号,化为分段形式,在每一个前提下去解不等式,每一步的解都要和前提条件找交集得出每一步的解,最后把每一步最后结果找并集得出不等式的解;根据第一步所化出的分段函数求出函数 的最小值,若
的最小值,若 ,使得
,使得 成立,只
成立,只
 ,解出实数
,解出实数 的取值范围.
的取值范围.
试题解析:(Ⅰ)当 时,
时, ,
, ,即
,即 ,
,
解得 ,又
,又 ,∴
,∴ ;当
;当 时,
时, ,
,
 ,即
,即 ,解得
,解得 ,又
,又 ,∴
,∴ ;当
;当 时,
时,
 ,
, ,即
,即 ,解得
,解得 ,又
,又 ,∴
,∴ .
.
综上,不等式 的解集为
的解集为 .
.
(Ⅱ) ,∴
,∴ .∵
.∵ ,使得
,使得 ,∴
,∴ ,整理得:
,整理得: ,解得:
,解得: ,
,
因此 的取值范围是
的取值范围是 .
.
考点:不等式;

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
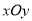 中,直线
中,直线 的方程为
的方程为 ,曲线
,曲线 的参数方程
的参数方程 (
( 为参数)
为参数)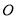 为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点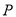 的极坐标
的极坐标 ,判断点
,判断点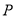 与直线
与直线 为曲线
为曲线 上的一个动点,求它到直线
上的一个动点,求它到直线
 B.
B.
 D.
D.
 中,
中, ,
, ,
, ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 的图象向右平移
的图象向右平移 个单位后得到函数
个单位后得到函数 ,则
,则 具有性质( )
具有性质( ) ,图象关于直线
,图象关于直线 对称
对称 上单调递增,为奇函数
上单调递增,为奇函数 上单调递增,为偶函数
上单调递增,为偶函数 ,图象关于点
,图象关于点 对称
对称 中,底面
中,底面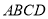 是菱形,
是菱形,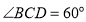 ,四边形
,四边形 是正方形,且
是正方形,且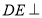 平面
平面
 平面
平面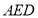 ;
; ,求多面体
,求多面体 的体积
的体积 .
. 的零点个数为( )
的零点个数为( ) ,经任意翻转二次后,点
,经任意翻转二次后,点 与其终结位置的直线距离不可能为( )
与其终结位置的直线距离不可能为( )
 B.
B. C.
C. D.
D.
 ,则
,则 的值为
的值为 B.0 C.1 D.2
B.0 C.1 D.2