题目内容
已知数列{an}具有性质:①a1为整数;②对于任意的正整数n,当an为偶数时,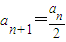 ;当an为奇数时,
;当an为奇数时,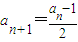 .
.(1)若a1=64,求数列{an}的通项公式;
(2)若a1,a2,a3成等差数列,求a1的值;
(3)设
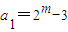 (m≥3且m∈N),数列{an}的前n项和为Sn,求证:
(m≥3且m∈N),数列{an}的前n项和为Sn,求证: .( )
.( )
【答案】分析:(1)由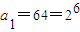 ,可得{an}的前7项成等比数列,从第8起数列的项均为0,从而利用分段函数的形式写出数列{an}的通项公式即可;
,可得{an}的前7项成等比数列,从第8起数列的项均为0,从而利用分段函数的形式写出数列{an}的通项公式即可;
(2)对a1进行分类讨论:若a1=4k(k∈Z)时;若a1=4k+1(k∈Z)时;若a1=4k+2(k∈Z)时;若a1=4k+3(k∈Z)时,结合等差数列的性质即可求出a1的值;
(3)由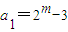 (m≥3),可得a2,a3,a4.若
(m≥3),可得a2,a3,a4.若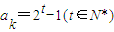 ,则ak是奇数,可得当3≤n≤m+1时,
,则ak是奇数,可得当3≤n≤m+1时,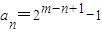 成立,又当n≤m时,an>0;当n≥m+1时,an=0.故对于给定的m,Sn的最大值为2m+1-m-5,即可证出结论.
成立,又当n≤m时,an>0;当n≥m+1时,an=0.故对于给定的m,Sn的最大值为2m+1-m-5,即可证出结论.
解答:解:(1)由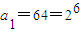 ,可得
,可得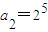 ,
,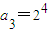 ,…,
,…,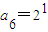 ,
,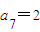 ,
,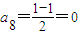 ,a9=0,…,
,a9=0,…,
即{an}的前7项成等比数列,从第8起数列的项均为0. …(2分)
故数列{an}的通项公式为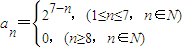 . …(4分)
. …(4分)
(2)若a1=4k(k∈Z)时,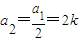 ,
,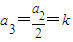 ,
,
由a1,a2,a3成等差数列,可知即2(2k)=k+4k,解得k=0,故a1=0;
若a1=4k+1(k∈Z)时,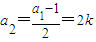 ,
,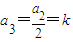 ,
,
由a1,a2,a3成等差数列,可知2(2k)=(4k+1)+k,解得k=-1,故a1=-3;…(7分)
若a1=4k+2(k∈Z)时,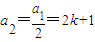 ,
,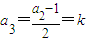 ,
,
由a1,a2,a3成等差数列,可知2(2k+1)=(4k+2)+k,解得k=0,故a1=2;
若a1=4k+3(k∈Z)时,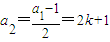 ,
,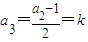 ,
,
由a1,a2,a3成等差数列,可知2(2k+1)=(4k+3)+k,解得k=-1,故a1=-1;
∴a1的值为-3,-1,0,2. …(10分)
(3)由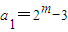 (m≥3),可得
(m≥3),可得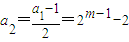 ,
,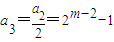 ,
,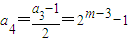 ,
,
若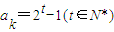 ,则ak是奇数,从而
,则ak是奇数,从而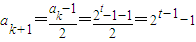 ,
,
可得当3≤n≤m+1时,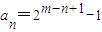 成立. …(13分)
成立. …(13分)
又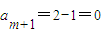 ,am+2=0,…
,am+2=0,…
故当n≤m时,an>0;当n≥m+1时,an=0. …(15分)
故对于给定的m,Sn的最大值为a1+a2+…+am=(2m-3)+(2m-1-2)+(2m-2-1)+(2m-3-1)+…+(21-1)=(2m+2m-1+2m-2+…+21)-m-3=2m+1-m-5,
故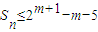 . …(18分)
. …(18分)
点评:本小题主要考查等差数列的性质、等比数列的性质、数列与函数的综合等基本知识,考查分析问题、解决问题的能力.
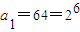 ,可得{an}的前7项成等比数列,从第8起数列的项均为0,从而利用分段函数的形式写出数列{an}的通项公式即可;
,可得{an}的前7项成等比数列,从第8起数列的项均为0,从而利用分段函数的形式写出数列{an}的通项公式即可;(2)对a1进行分类讨论:若a1=4k(k∈Z)时;若a1=4k+1(k∈Z)时;若a1=4k+2(k∈Z)时;若a1=4k+3(k∈Z)时,结合等差数列的性质即可求出a1的值;
(3)由
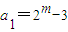 (m≥3),可得a2,a3,a4.若
(m≥3),可得a2,a3,a4.若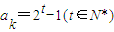 ,则ak是奇数,可得当3≤n≤m+1时,
,则ak是奇数,可得当3≤n≤m+1时,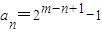 成立,又当n≤m时,an>0;当n≥m+1时,an=0.故对于给定的m,Sn的最大值为2m+1-m-5,即可证出结论.
成立,又当n≤m时,an>0;当n≥m+1时,an=0.故对于给定的m,Sn的最大值为2m+1-m-5,即可证出结论.解答:解:(1)由
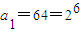 ,可得
,可得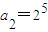 ,
,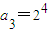 ,…,
,…,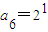 ,
,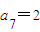 ,
,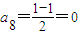 ,a9=0,…,
,a9=0,…,即{an}的前7项成等比数列,从第8起数列的项均为0. …(2分)
故数列{an}的通项公式为
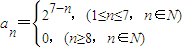 . …(4分)
. …(4分)(2)若a1=4k(k∈Z)时,
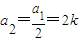 ,
,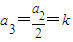 ,
,由a1,a2,a3成等差数列,可知即2(2k)=k+4k,解得k=0,故a1=0;
若a1=4k+1(k∈Z)时,
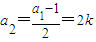 ,
,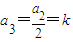 ,
,由a1,a2,a3成等差数列,可知2(2k)=(4k+1)+k,解得k=-1,故a1=-3;…(7分)
若a1=4k+2(k∈Z)时,
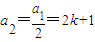 ,
,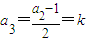 ,
,由a1,a2,a3成等差数列,可知2(2k+1)=(4k+2)+k,解得k=0,故a1=2;
若a1=4k+3(k∈Z)时,
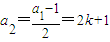 ,
,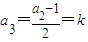 ,
,由a1,a2,a3成等差数列,可知2(2k+1)=(4k+3)+k,解得k=-1,故a1=-1;
∴a1的值为-3,-1,0,2. …(10分)
(3)由
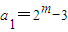 (m≥3),可得
(m≥3),可得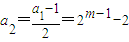 ,
,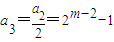 ,
,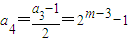 ,
,若
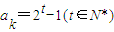 ,则ak是奇数,从而
,则ak是奇数,从而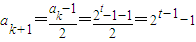 ,
,可得当3≤n≤m+1时,
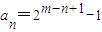 成立. …(13分)
成立. …(13分)又
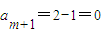 ,am+2=0,…
,am+2=0,…故当n≤m时,an>0;当n≥m+1时,an=0. …(15分)
故对于给定的m,Sn的最大值为a1+a2+…+am=(2m-3)+(2m-1-2)+(2m-2-1)+(2m-3-1)+…+(21-1)=(2m+2m-1+2m-2+…+21)-m-3=2m+1-m-5,
故
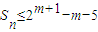 . …(18分)
. …(18分)点评:本小题主要考查等差数列的性质、等比数列的性质、数列与函数的综合等基本知识,考查分析问题、解决问题的能力.

练习册系列答案
相关题目
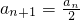 ;当an为奇数时,
;当an为奇数时,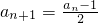 .
.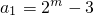 (m≥3且m∈N),数列{an}的前n项和为Sn,求证:
(m≥3且m∈N),数列{an}的前n项和为Sn,求证: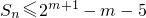 .
.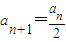 ;当an为奇数时,
;当an为奇数时,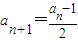 .
.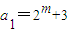 (m>3且m∈N),数列{an}的前n项和为Sn,求证:
(m>3且m∈N),数列{an}的前n项和为Sn,求证: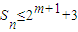 ;
;