题目内容
14.已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1\\ f({x-1})\end{array}\right.$$\begin{array}{l}{x≤0}\\{x>0}\end{array}$,则下列命题中:(1)函数f(x)为周期函数;
(2)函数f(x)在区间(m,m+1)(m∈N)上单调递增;
(3)函数f(x)在x=m-1(m∈N)取到最大值0,且无最小值;
(4)若方程f(x)=loga(x+2)(0<a<1)有且只有两个不同的实根,则$a∈[{\frac{1}{3},\frac{1}{2}})$.
正确的命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 作出f(x)的图象,由图象对各选项进行判断即可.x≤0时,$y=-{2}^{-x}+1=-(\frac{1}{2})^{x}+1$,可由$y=(\frac{1}{2})^{x}$的图象作关于x轴的对称图象,再向上平移一个单位得到.
解答 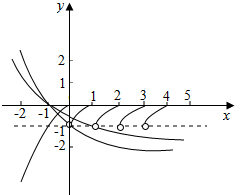 解:f(x)的图象如图所示:
解:f(x)的图象如图所示:
(1)∵f(-1)=-1≠f(0)=0,故(1)不正确;
(2)由图可知(2)正确;
(3)∵m=0时,f(m-1)=f(-1)=-1,不是最大值,故(3)不正确;
(4)如图(2)所示,图中两条曲线对应的a分别为$\frac{1}{3}$和$\frac{1}{2}$,故方程f(x)=loga(x+2)(0<a<1),有且只有两个实根,则a∈[$\frac{1}{3}$,$\frac{1}{2}$),故(4)正确.
∴正确命题的个数是2个.
故选:B.
点评 本题考查分段函数的性质、方程的根等知识,综合性较强,考查利用所学知识解决问题的能力,是中档题.

练习册系列答案
相关题目
2.一个袋子中有号码为1,2,3,4大小相同的4个小球,现从中任意取出一个球,取出后再放回,然后再从
袋中任取一个球,则取得两个号码之和为5的概率为( )
袋中任取一个球,则取得两个号码之和为5的概率为( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{16}$ |
6.已知a=$lo{g}_{\frac{1}{3}}{2}^{-1}$,b=ln2,c=${5}^{-\frac{1}{2}}$,则( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
4.从某高校男生中随机抽取100名学生,测得他们的身高(单位:cm)情况如下表:
(Ⅰ)求a,b,c的值;
(Ⅱ)按表中的身高组别进行分层抽样,从这100名学生中抽取20名担任某国际马拉松志愿者,再从身高不低于175cm的志愿者中随机选出两名担任迎宾工作,求这两名担任迎宾工作的志愿者中至少有一名的身高不低于180cm的概率.
| 分组 | 频数 | 频率 |
| [160,165) | 10 | 0.10 |
| [165,170) | 30 | 0.30 |
| [170,175) | a | 0.35 |
| [175,180) | b | c |
| [180,185] | 10 | 0.10 |
| 合计 | 100 | 1.00 |
(Ⅱ)按表中的身高组别进行分层抽样,从这100名学生中抽取20名担任某国际马拉松志愿者,再从身高不低于175cm的志愿者中随机选出两名担任迎宾工作,求这两名担任迎宾工作的志愿者中至少有一名的身高不低于180cm的概率.